t検定 ２つのグループの平均に差はあるのかそうじゃないか調べる手法 平均に差がない場合 95%、または99%の確率で起こりえる差なのでその平均の差に意味はない 平均に差がある場合 グループの平均の差は評価の差に意味はある グループが3つ以上あるとt検定は使えない このページで利用する公式 差の標準誤差 推定母分散が標本Aと標本B …
平均差の信頼区間とt検定[NOINDEX]
カテゴリー: 統計学
区間推定と信頼区間
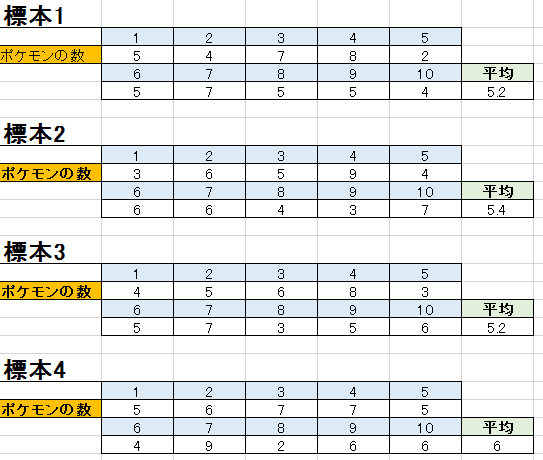
母集団の平均と分散を推定する 日本中の人= 母集団 日本中の人のポケモン所持数の平均を知りたい でもそれは現実的ではないから、標本のデータから母集団の平均を統計(確率)から推定することが出来ます 推計統計の手法を使うと、標本から母集団を確率から推計出来ます。 標本 路上を歩いている人を10人を1標本として平均を求めることにする 標本4つ分のデータを集めた …
標準正規分布と確率密度関数
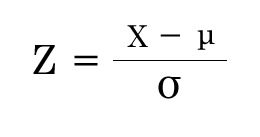
標準化 変数変換 X － μを行うことで、真ん中を平均μからずらして0(真ん中)に移動させます σで偏差X － μで割ることでσ = X － μの時に1となる、 標準正規分布に変換出来ます。 例 Aくんの音楽の点数：80点 平均：60点 標準偏差：10点 一峰性があり正規分布である時に、 点数を平均で引くと偏差 標準正規分布の標準偏差は1 偏差を標準偏差 …
共分散と相関比
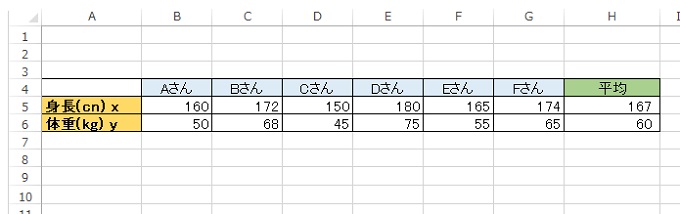
データの例 身長と体重のデータを用意しました、 身長と体重において相関関係があるかを共分散と相関係数を求めることでみていきます。 共分散Sxy 相関係数の公式 共分散はXの偏差を一辺、Yの偏差で一辺をとる長方形の面積の平均と考えることが出来ます。 相関係数を出してみよう 相関係数の目安 0.7 ～ 1.0 かな …
2乗すること、√を付与するということ
結論 nを２乗する = 1辺がnの正方形の面積 nを√にする = 面積がnである正方形の一辺の長さ １辺が12cm, 一辺が3cmの長方形の面積 12 × 3 = 36cm^2の長方形になります。 これに√をつけると √36 = 6 この6ってなに？ 36cm^2の長方形を正方形と見た時 = 1辺を平 …
二項分布 多項分布
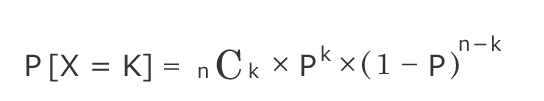
二項分布 ex) 表の確率が20%, 裏が80%の確率で出る特殊なコインを5枚投げて、表が３枚出る確率 ex) 赤玉１つ、青玉2つ、白玉3つが入っている抽選機があり、一度抽選を引くたびに玉は戻すとします。3回抽選を行った時に赤玉が2つ出る確率 多項分布 ex) 赤玉１つ、青玉2つ、白玉3つが入っている抽選機があ …
ベイズの定理
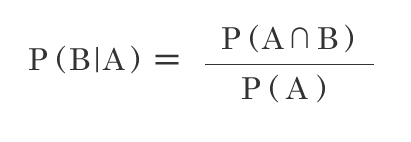
条件付き確率 確率P(A)が起こるとした時の、確率P(B)が起こる確率を表します。 ex) サイコロを振った時に奇数だった時に、5以上である確率 ベイズの定理 条件付き確率を変形させるとベイズの定理を導出出来ます。 ベイズの定理導出 ① ② ③ ①を変形して③になる ③を②に代入します。 ベイズの定理になります …
標本誤差
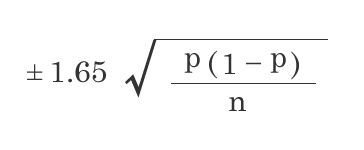
比率の標本誤差 推計統計学で、とある標本のデータから母集団の値を推計します。 視聴率というものがありますが、日本の全世帯を調査するのは大変ですよね。わずかなサンプル数、今回だと600世帯のサンプルの視聴率から標本誤差を利用すると、全世帯の視聴率(母集団)を確立的に推計することが出来ます。 90%信頼度の比率の標本誤差 95%信頼度の比率の標本 …
疑似相関
疑似相関 一見すると関係がありそうだけれど、直接の関係にない見掛けの相関関係にあるが、直接の因果関係は別の要因(潜在変数)によるものであるケース。 例1. 声の高低と指輪のサイズ 声の低い人ほど指輪のサイズが大きく、 声が高い人ほど指輪のサイズが小さかった 声の高低と指輪のサイズは相関関係がある？ ⇒性別が直接の要因 例2. お米を食べた …
中央値, 四分位範囲, 四分位偏差, はずれ値
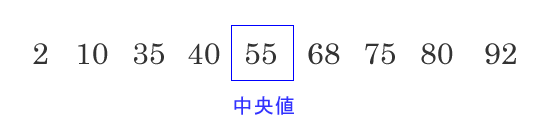
中央値(メジアン) サンプル数が奇数の場合 サンプル数が偶数の場合 中央の数値２つの平均を中央値とします。 四分位数(ヒンジ), 四分位範囲(IQR) 第1四分位点（Q1） 第2四分位点（Q2） 第3四分位点（Q3） 四分位範囲(IQR) = 第３四分位数(Q3) － 第 …
平均値, 中央値, 最頻値
正規分布でつりがね型のデータ分布の時に、平均値と中央値が綺麗に出やすい。 平均値と中央値の値のずれがあまりなければ平均値が使いやすい。 最頻値と中央値は外れ値の影響を受けにくい 平均値 データの総和をサンプル数で割ったもの、算術平均。 メリット データが更新されると平均値も影響を受け更新される デメリット 極端に低い値、高い値の …
期待値
期待値は確率×確率変数の総和 サイコロを１回振った時の期待値 確率変数 1 2 3 4 5 6 確率 1/6 1/6 1/6 1/6 1/6 1/6 1×1/6 + 2×1/6 + 3×1/6 + 4×1/6 + 5×1/6 + 6×1/6 =1/6 + 2/6 + 3/6 + 4/6 + 5/6 + 6/6 = 3.5 10万円が1本、1万 …