Python 偏微分で大満足カレーを作る Matplotlib 寄稿しました。 大満足カレー物語 いつでも美味しく食べられる国民食”ドンカレー”の成功で大富豪と知られるシファーナさんが街で小さなインドカレー屋を営んでいた時のお話。 新製品の開発を考えた結果、カレーのとろみ度とスパイス量が満足度に直結するのではないかとシファーナさんは考えました。そこでカレー …
Python 偏微分で大満足カレーを作る
カテゴリー: 統計学
モンティホール問題とベイズの定理
ルール A, B, Cの扉の先に正解がある まずゲストはA, B, Cのいずれかの扉を選ぶ 正解の扉を知っている司会がはずれの扉を１つ選ぶ ゲストは残った２つの扉のどちらかを改めて選ぶことが出来る権利を与えられる 命題 ゲストは最初の扉の選択を変更した方が良いのか？ 司会からはずれの情報を得た前後で確率は変化するのか？ どう選ぶのが確率として高いのか ・選んだ扉から変更 …
協調フィルタリング cos(コサイン)類似度
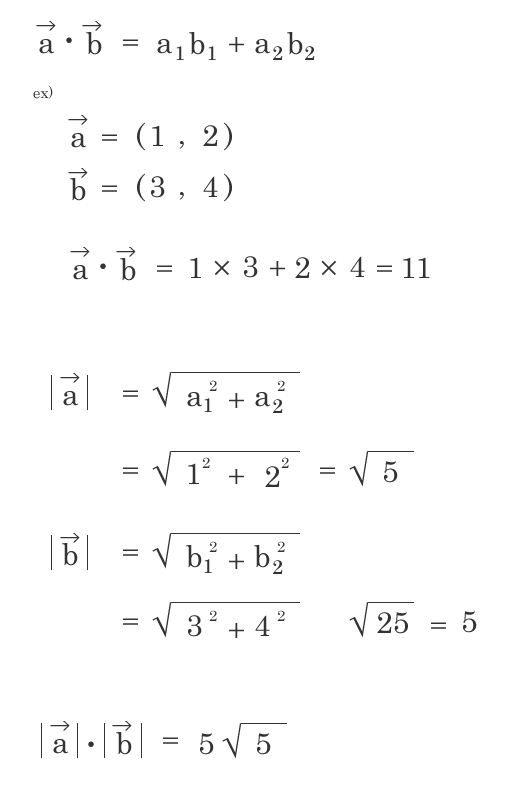
グループ分けを行い、各グループの類似度をベクトルの内積の公式を使って、cosθの値で類似度を判断する。 類似度が高い･･･似てるほど1に近づく、類似度100%で1 類似度が低い･･･似てないほど0に近づく、類似度0%で0 補足1. ベクトルの基本的なところ 補足2. ベクトルの内積の公式 a, bベクトルのなす角θ …
k近傍法 k-nearest neighbor algorithm, k-NN
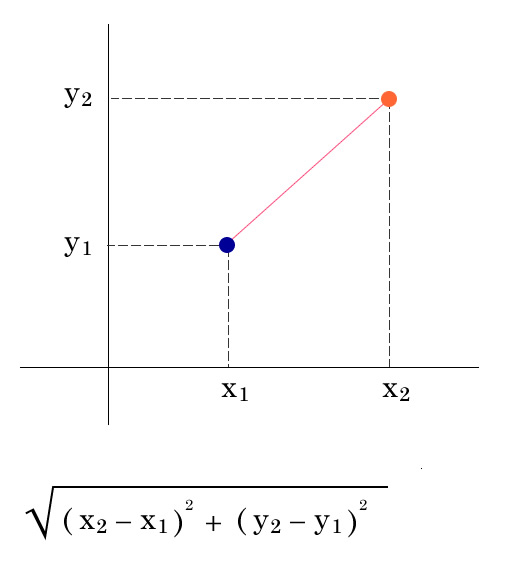
k近傍法 データのカテゴリが近いかどうかを距離でどれだけ属性が近いかを評価し分類。 レコメンドアルゴリズムの１つ。 評価項目が２つ(2次元、ユークリッド平面) ２つのデータが似ているかどうかを距離で評価する、 三平方の定理でデータの最短距離の直線、 2次元のユークリッド距離が出せます。 シンプルな直線。 ex) 評価項目が５つあ …
カイ(χ)二乗値とカイ二乗検定
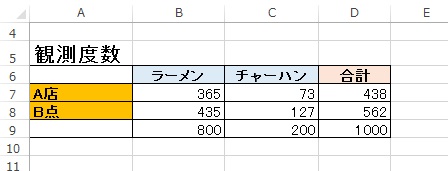
前提 A店のラーメンとチャーハンのそれぞれの販売数、 これは他の御店と売れ行き方に差があるのか知りたい A店とB店のラーメンとチャーハンの販売数から、 A店のラーメンとチャーハンの売れ行き方に他の店と差があるのか、ないのかを知る 仮説検定 データの有意度を判定を行うために帰無仮説を立てます。 A店とB店のラーメンとチャーハンの販売数について差はないという仮説 = 帰無仮 …
テイラー展開+マクローリン展開で近似
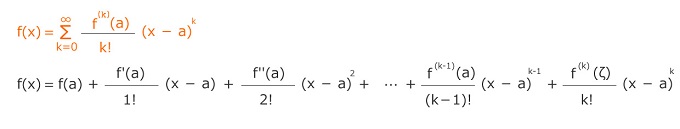
テイラー展開 元の式 ＝ f(a) + １階微分 + ２階微分 + ･･･ + n階微分した総和 数があまりに小さい時に近似として使える。 物理学・統計学、三角関数等を簡単な近似の式にする。 exp) (1.008)^20 0次近似 1.008^20はほとんど１と同じという考え 1.008^20 ≒ 1^20 ≒ 1   …
Excelで単回帰分析
Excelで単回帰分析 データを分析して未来を予測しちゃおう！ 寄稿しました。 作業フロー まずは月別の売上高の棒グラフを作成してみる xとyとして相関しそうな２つのデータを見つける ２つの相関比を計測する →相関関係がない おしまい、他のデータを見よう。 ２つのデータから散布図を作成する 単回帰分析で１次関数を割り出す １次関数を使って未来を予測する こんな流れでやっていきます。 …
数学や統計学でのギリシャ文字と記号の意味
ε(イプシロン) とても小さな正の数 いくらでも０に近付けられる正の数 導関数を説明する時のhとεは同じ意味だよ。 Δ(デルタ) 変数の前につけると、『その変数のわずかな変化』の意味 Δxは 『変数xのわずかな変化』, 『(x1-x0), (x2-x1)など、ｘから次の点までの距離』 Δx = dx, 導関数のh=Δx f'(x)=Δy/Δx=dy/dx 微分のdy/d …
等差数列, 等比数列
「初項と末項を足して２で割ると総和」の考え方 3+5+7+9+11+13+15 = 63 15+13+11+9+7+5+3=63 (18 × 7) ÷ 2 = 63 求めたい等差数列と反転させた数列を用意します ２つの等差数列を足すと平均値の18が出る 初項と末項を足し合わせた形、2項目を足しあわる・・・n 平均値18と項数7を掛け 求めたい数列の和は1列分なので、2で割ると綺麗に総 …
分散分析とF分布表[NOINDEX]
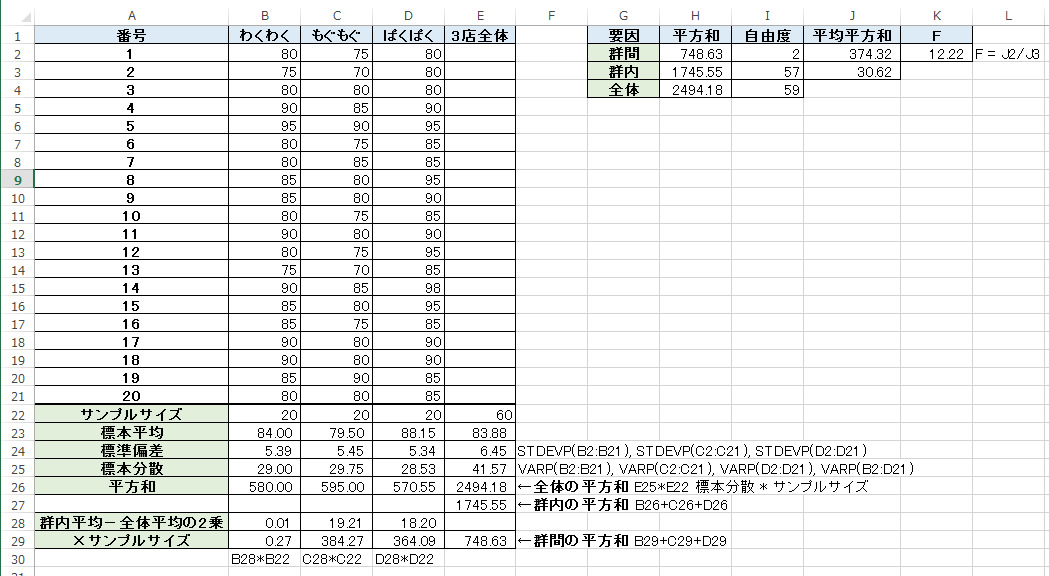
全体の平均からのずれ = 群間のずれ + 群内のずれ 群間の自由度 = 群の数 － 1 群内の自由度 = (群1のサンプルサイズ － 1) + (群2のサンプルサイズ － 1) + (群3のサンプルサイズ － 1) 全体の自由度 = 各群のデータを合わせたサンプルサイズ － 1 F値 = 群間の平均平方 / 群内の平均平方 信頼区間、有意水準の考え方 有意水準0.05 …
偏微分で最小二乗法 単回帰分析
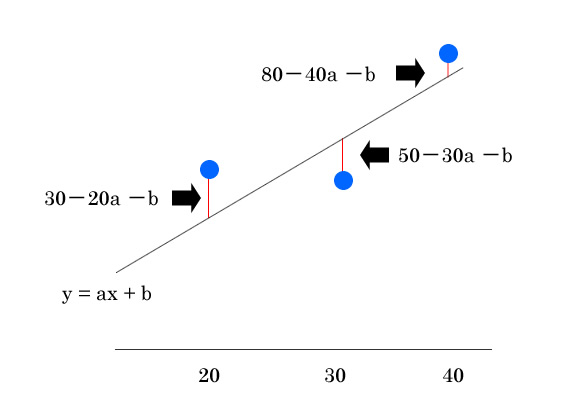
気温℃ 20 30 40 アイスの販売個数 30 50 80 目的 気温をx、アイスの個数yとして、売上予測をするための一次関数を導く 効用 「気温があがればアイスも売れるよなぁ」をデータから直線に出来る 直線が出来たら気温から今後の販売数を予測出来る 最小二乗法から出す方法 上記は理想となる一次関数の残差の合計、差の値によって－になるから2 …
単回帰分析の傾きとy切片
傾き y切片 Amazonおすすめ iPad 9世代 2021年最新作 iPad 9世代出たから買い替え。安いぞ！🐱 初めてならiPad。Kindleを外で見るならiPad mini。ほとんどの人には通常のiPadをおすすめします＞＜