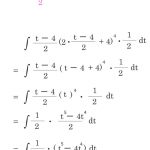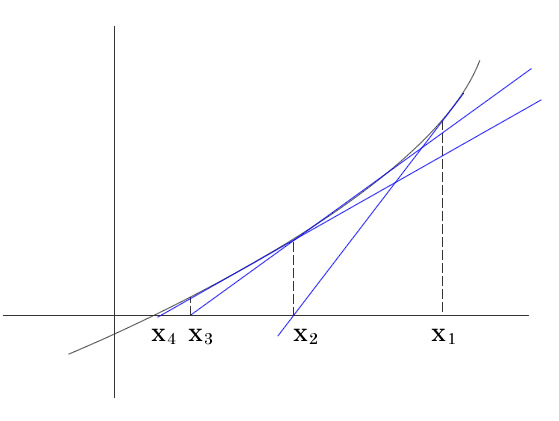
- ①適当に決めたX1の時の接線からy = 0との交点X2を見出す、X2の時の接線からy = 0との交点X3を見出す・・・×n
- ②X1からスタートして①を繰り返していく
- ③X1からX2, X2からX3, X3からX4とどんどん距離が短くなって・・・解に近づいていく。
→解の近似が求められる
もくじ
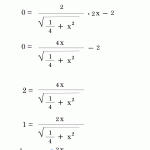
ニュートン法の導出
- f(x)の微分すると導関数のf ‘(x)が出る
- 導関数f ‘(x)にX1を入れるとf ‘(X1)、X1の時の 「傾き(微分係数)」が出る。
- 微分係数と傾きの定義の関係を利用して導出します。
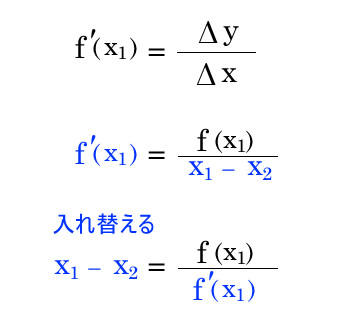
@see 優技録 分数の式変形
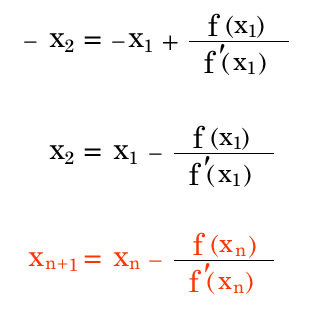
漸化式が出来た。
これをループさせていくと目的の解に限りなく近くなる→近似が出る
これをニュートン法と呼びます。
ニュートン法の良いところ
- 4次、5次・・・高次の関数でも解の近似が出せる。
- 3次以上の関数は数学の問題のように綺麗に解が出せる場合が少ない
→ 現実の世界で利用するなら近似で十分 - 何度もループして計算するのが大変じゃない?
→ コンピュータさんにループ計算で頑張って貰う、一瞬!
// 解の近似として十分とする誤差の閾値を設定してループを終了させる
近似?近似解って何?
- 0.999はほぼ「1」という考え方
- 500mlジュースの例
実際には498mlしかジュースが入ってなかったとしても誰もクレームは入れない。厳密ではないけれど問題にならない。 - 海外旅行の例
「あれがこうで、98,300円かかるかな?でも実際に旅行してみないと本当のことはわからないよな・・・もっと調べなくちゃ!」より、
「だいたい10万円だな、何があるかわからないし15万円持っていけば大丈夫だろう」の方が仕事が出来る人っぽいでしょう?
私達は近似を利用して“だいたい合ってる”バランス感で生きている。
隕石が飛んできて明日死ぬかもしれない、確率が小さいものはほぼ「0」と考える。小さすぎるものは生きる上で無視できる。
気をつける
- 高次の関数で一つだけ解を出してそれを極値と勘違いしないこと
極大、極小となる候補の1つに過ぎない - 微分して0となる箇所(頂点)が複数出る
- それぞれの解で計算して値を比較することで極大値、極小値を判断する
使い方
- 最大利益の計算
- 最大満足度の計算
- 最適化の計算
関数の作り方
データを散布図でプロットして最小二乗法で割り出す(コンピュータさんが頑張る)
- データを散布してプロットする(コンピュータさんが頑張る)
- 二乗和を求める(コンピュータさんが頑張る)
- 偏微分する(コンピュータさんが頑張る)
- 連立方程式で割り出す(コンピュータさんが頑張る)
@see 優技録 最小二乗法
製造の利益計算の例
- 利益y = 生産力とコストを利用してモデルとなる関数を作る
// 利益 = 生産 -コスト - 微分して0となる解 = 最大利益(最小利益)を決めるxを求める
→ニュートン法で近似を出す
3次関数の解の見つけ方
- 一般的に3次関数の解は3つ
- 初期値のポイントを0, 5, 10, 15, 20など分散させてニュートン法を行う
- 3つの解に収束する
解が収束しない例
import matplotlib.pyplot as plt import numpy as np x = np.arange(-2,2,0.01) y = x**3 -2*x + 3 plt.figure(figsize=(20, 10), dpi=50) plt.plot(x,y, color = "black") plt.show()
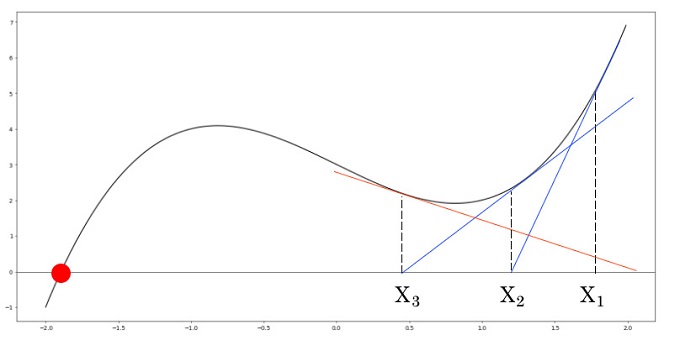
初期値をX1とした時に、 X2と来て、X3で戻ってしまうので収束しない
無限ループを見切る
- ループする度に|X1 - X2|の絶対値の差が0.001以下になった時
- 最大試行回数を決めておく
解が収束しないなど無限ループを防止する仕組み、ループから抜ける収束条件を忘れずに設定しておく。
生半なプログラムを実行してからでは不可避なのだ、発動前に見切ること。
Python Numpyで計算しよう
√3の割り出し
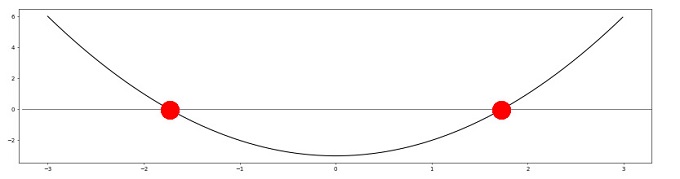
√3って何?
√3は2乗すると3になる数 ・・・
√3って具体的に何なの?よくわからないものはXとおく。
Xを二乗すると3になるよ!とする
X^2 = 3
次に変形して、=0の形にする
X^2 -3 = 0
X^2 −3をf(x)とします、それが=0となる時だから
f(x) = X^2 -3 = 0
この関数が= 0となるXが何なのか?
これが√3の正体。
→だからニュートン法で計算する。
√3はこれだっていうのは出せないが、近いものは出せる →近似解
import matplotlib.pyplot as plt
import numpy as np
initialValue = float(4) # 初期値
min = 0.001 # 微小な数
attemptLimits = 500 # 最大試行回数
# 解を求める関数
def targetFunc(x):
return x**2 -3.0
# 導関数
def derivative(x):
return 2.0*x
def newtonMethod(a, min):
for i in range(attemptLimits):
# 漸化式
ah = a - targetFunc(a)/derivative(a)
# 収束条件
if abs(a - ah) < min:break
# 近似解の更新
a = ah
return a, i
def main():
a, i = newtonMethod(initialValue, min)
print("解:",a ,"試行回数:", i+1)
if __name__ == '__main__':
main()
解: 1.7320520571470122 試行回数: 5
利益計算、高次関数の近似解の割り出し
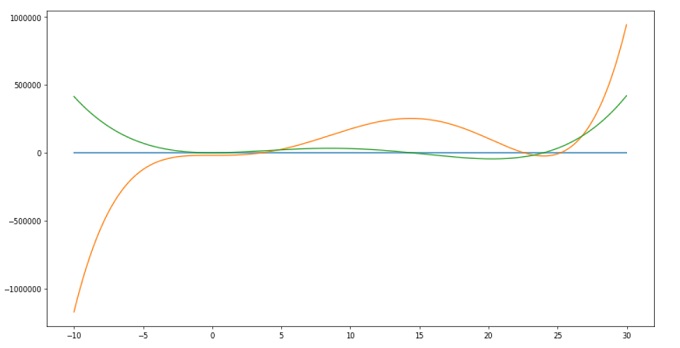
とある工場の生産での利益計算を行った結果、関数f(x) = X^5 -48X^4 +576X^3 -200X -19200を導いた、これを利用して最大利益を計算したい。ただし、Xは−10~24.5までの範囲とする。
- 導関数f ‘(x)が = 0になる時がf(x)が最大になる
f ‘(x) = 5x^4 -192x^3 +1728x^2 -200 - 導関数f ‘(x)を更に微分してf ”(x)を求める
f ”(x) = 20x^3 -576x^2 +3456x - f ‘(x)=0の解をf ”(x)を使ってニュートン法を使って求める
f(x) = 5x^4 -192x^3 +1728x^2 -200
import matplotlib.pyplot as plt import numpy as np x = np.arange(-10,30,0.01) y = x**5 -48*x**4 +576*x**3 -200*x -19200 plt.figure(figsize=(15, 8), dpi=50) plt.plot(x,y) plt.show()
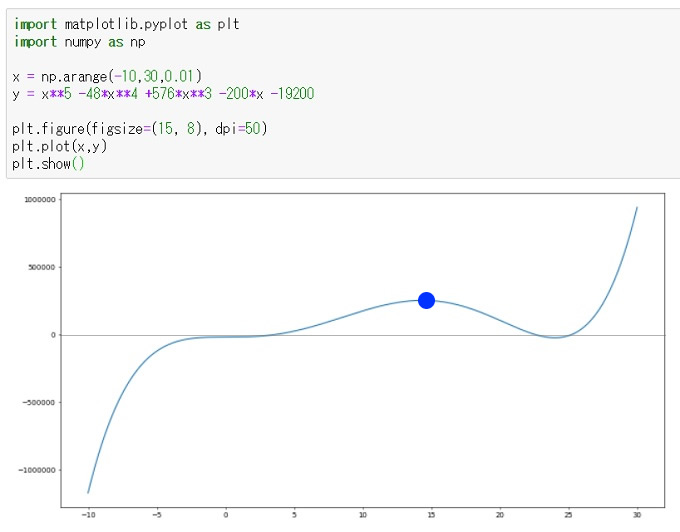
青の利益を出せるXを求めたい。
導関数 f ‘(x) = 5x^4 -192x^3 +1728x^2 -200
import matplotlib.pyplot as plt import numpy as np x = np.arange(-10,30,0.01) y = 5*x**4 -192*x**3 +1728*x**2 -200 plt.figure(figsize=(15, 8), dpi=50) plt.plot(x,y) plt.show()

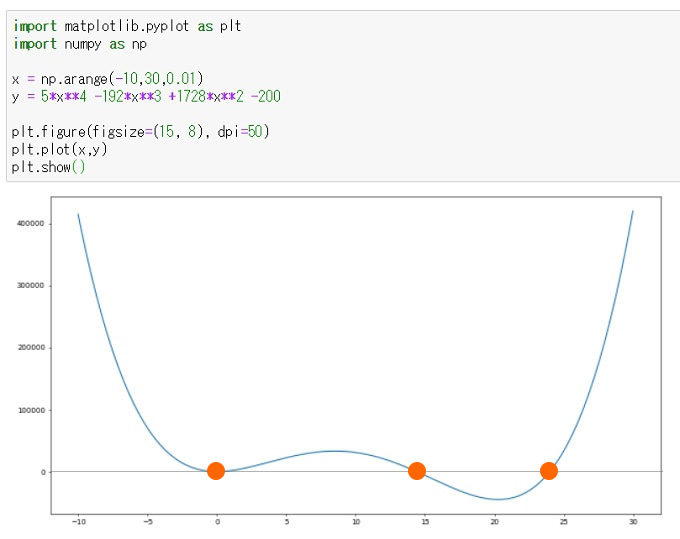
f ‘(x) = 0の時の解がf (x)の極大(極小)となる候補になる。f (x)とf ‘(x) のグラフを見比べると、X≒14の解が極大となることがわかります。
・・・そうなると話が終わってしまうので、f ‘(x) をさらに微分したf ”(x)を利用して、f ‘(x) = 0となる解をニュートン法で求めます。
整理する
- f ‘(x) = 5x^4 -192x^3 +1728x^2 -200
- f ”(x) = 20x^3 -576x^2 +3456x
f ‘(x) = 0となる解をニュートン法で求めるよ!
import matplotlib.pyplot as plt
import numpy as np
initialValue = float(5) # 初期値
min = 0.00001 # 微小な数
attemptLimits = 500 # 最大試行回数
# 解を求める関数
def targetFunc(x):
return 5*x**4 -192*x**3 +1728*x**2 -200
# 導関数
def derivative(x):
return 20*x**3 -576*x**2 +3456*x
def newtonMethod(a, min):
for i in range(attemptLimits):
# 漸化式
ah = a - targetFunc(a)/derivative(a)
# 収束条件
if abs(a - ah) < min:break
# 近似解の更新
a = ah
return a, i
def main():
a, i = newtonMethod(initialValue, min)
print("解:",a ,"試行回数:", i+1)
if __name__ == '__main__':
main()
| 初期値 | f ‘(x)の解 |
| 5 | 0.34689681750956386 |
| 10 | -0.33401431362403844 |
| 15 | 14.379894550359529 |
| 20 | -0.33401247268531953 |
| 25 | 24.007226797593827 |
ここで4つの解が出る。
利益計算する
f(x) = 5x^4 -192x^3 +1728x^2 -200に f ‘(x)の解を代入して比較する
import matplotlib.pyplot as plt
import numpy as np
x = float(-0.33401247268531953) # f'(x)の解を代入しよう!
def targetFunc(x):
return x**5 -48*x**4 +576*x**3 -200*x -19200
def main():
val = targetFunc(x)
print("利益:",val)
if __name__ == '__main__':
main()
| f (x) | 利益 |
| -0.33401247268531953 | -19155.26309352801 |
| 0.34689681750956386 | -19246.024507207505 |
| 14.379894550359529 | 253110.29576736654 |
| 24.007226797593827 | -24000.72272655742 |
−10≦ x ≦24.5の時に、f(14.379894550359529)の時に最大利益 253110.29576736654となる。
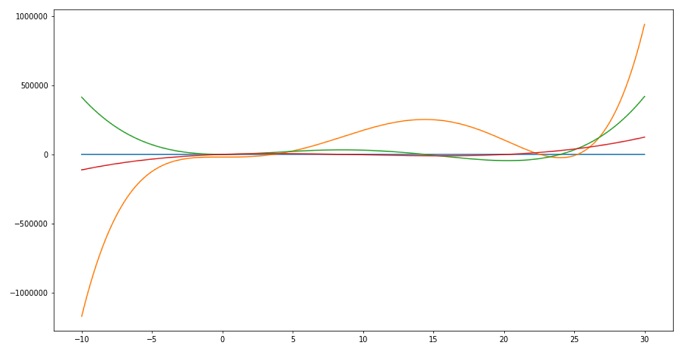
import matplotlib.pyplot as plt import numpy as np x = np.arange(-10,30,0.01) y0 = 0*x # y = 0 y = x**5 -48*x**4 +576*x**3 -200*x -19200 # f(x) yp = 5*x**4 -192*x**3 +1728*x**2 -200 # f'(x) ypp = 20*x**3 -576*x**2 +3456*x # f''(x) plt.figure(figsize=(15, 8), dpi=50) plt.plot(x,y0) plt.plot(x,y) plt.plot(x,yp) plt.plot(x,ypp) plt.show()
また、X ≒ 24の解を超えると指数関数的に爆益していく。