ｘを共有する異なる関数は、関数同時の和や積などを求めることが出来ます。

 

２つの関数の最大となるｘを求めるには

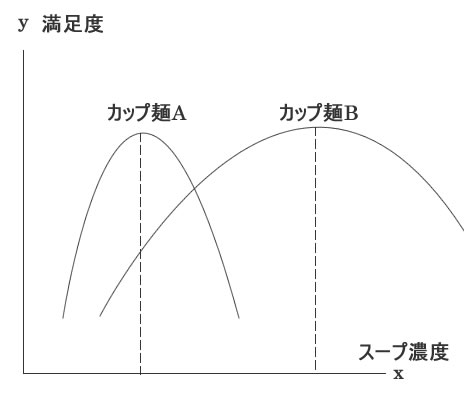
スープ濃度を変数ｘとして、カップ麺A, カップ麺Bの満足度が最大になるxを求めたい。

スープ濃度xを共通した時のf(x)とg(x)の和、”f(x)+g(x)”が最大のポイント。

 

カップ麺A, カップ麺Bがそれぞれ最大の満足度になるxの位置は異なる。和が最大のポイントを求める。

関数の和”f(x)+g(x)”を１つの関数とみなし、微分して0を使う。

和の微分

$$\left\{ f\left( x\right) +g\left( x\right) \right\} ^{‘}=f’\left( x\right) +g’\left( x\right)$$

足してから微分するか、微分してから足す。

 

カップ麺Aの販売個数をf(x)=-5x^2+2x+5

カップ麺Bの販売個数をg(x)=-2x^2+x+2

 

とした時。和の微分

 

$$\left\{ f\left( x\right) +g\left( x\right) \right\} ^{‘}=f’\left( x\right) +g’\left( x\right)$$

$$\begin{align*} & =\left( -10x+2\right) +\left( -4x+1\right) \\ & =14x+3\\ & 0=14x+3\\ & x=\dfrac {3} {14}\end{align*}$$

 

 

売上額を(販売個数×単価)を最大にするポイント

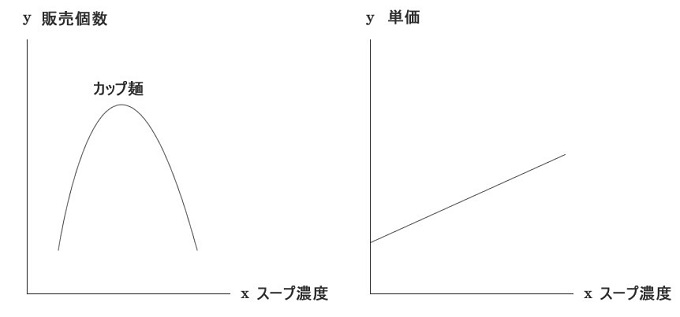
次数が異なるグラフに対しても計算は可能です。

スープ濃度をあげて売上額が最大になるポイントを見つけたい。

積の微分

$$\left\{ f\left( x\right) \times g\left( x\right) \right\} ^{‘}=f’\left( x\right) +g\left( x\right) +f\left( x\right) +g’\left( x\right)$$

スープ濃度xの時の販売個数をf(x) = -5x^2+2x+5,

単価を g(x) = x+2

とする。

この２つの積の微分し、y=0となる地点のxが頂点になります。

 

$$\left\{ f\left( x\right) \times g\left( x\right) \right\} ^{‘}=f’\left( x\right) +g\left( x\right) +f\left( x\right) +g’\left( x\right)$$

$$\begin{align*} & =\left( -10x+2\right) \times \left( x+2\right) +\left( -5x^{2}+2x+5\right) \times 1\\ & =-15x^{2}-16x+9\end{align*}$$

 

２次関数の解の公式より、

$$\begin{align*} & 0=-15x^{2}-16x+9=0\\ & 15x^{2}+16x-9=0\\ & x=\dfrac {-16\pm \sqrt {16^{2}-4\times \left( -9\right) }} {2\times 15}=\frac {-16\pm \sqrt {796}} {30}\end{align*}$$

 

ｘが-は今回はありえないので、

$$\begin{align*} & x=\dfrac {-16+\sqrt {796}} {30}\\ & =0.4071\end{align*}$$

x=0.4071の時、売上額が最大となる。

 

@see 微分積分入門