もくじ
前提
- A店のラーメンとチャーハンのそれぞれの販売数、
これは他の御店と売れ行き方に差があるのか知りたい - A店とB店のラーメンとチャーハンの販売数から、
A店のラーメンとチャーハンの売れ行き方に他の店と差があるのか、ないのかを知る
仮説検定
- データの有意度を判定を行うために帰無仮説を立てます。
- A店とB店のラーメンとチャーハンの販売数について差はないという仮説 = 帰無仮説
- 差はないとしてカイ二乗値を求め、差がない場合にどれだけの確率でそのカイ二乗値が出るのかをカイ二乗分布表から有意水準5%で判定することにします
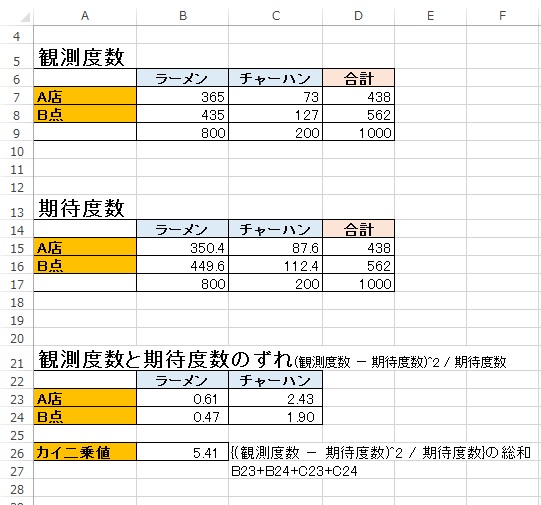
観測したデータ
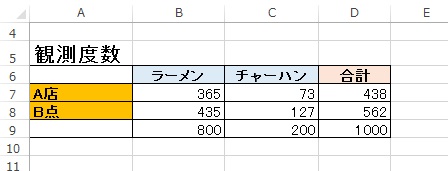
ラーメン:チャーハン = 800 : 200
= ラーメン:チャーハン = 0.8 : 0.2
A店とB店の合算した売上の比率から、
ラーメンとチャーハンの割合は8:2で売れるようです。
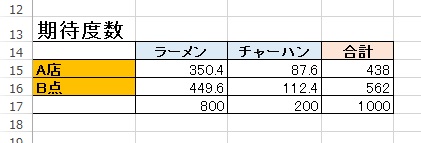
比率を元に期待度数をあてはめるとこうなります。
- A店のラーメンの期待度数 = 438 × 0.8 = 350.4
- A店のチャーハンの期待度数 = 438 × 0.2 = 87.6
- B店のラーメンの期待度数 = 562 × 0.8 = 449.6
- B店のチャーハンの期待度数 = 562 × 0.2 = 112.4
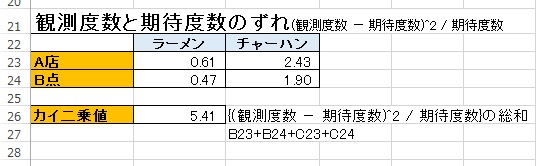
観測度数と期待度数のずれを計上します。
ずれ
(観測度数 - 期待度数)^2 / 期待度数 = ずれ
カイ二乗値
{(観測度数 - 期待度数)^2 / 期待度数}の総和 = カイ二乗値
今回のデータの自由度
行数2、列数2なので、
自由度 = (行数2 - 1) × (列数2 - 1)
= 1 × 1
= 1
今回のデータの自由度は1になります
カイ二乗分布表から仮説検定を行う
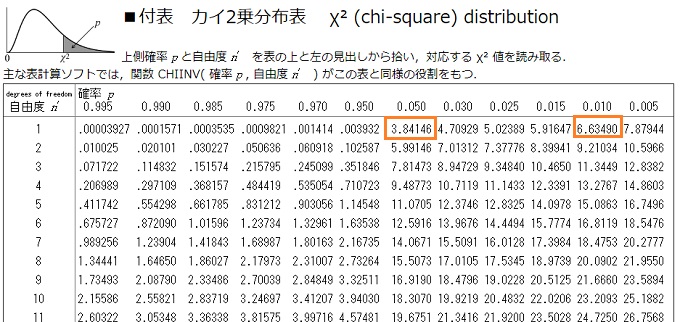
@see https://www.biwako.shiga-u.ac.jp/sensei/mnaka/ut/chi2disttab.html
検定していこ~!
自由度1、カイ二乗値5.41をもって、
0.05 = 有意水準5%のカイ二乗分布表の箇所を見て行きます。
データに差がない時に、カイ二乗値5.41が発生するのは5% ~ 1%の間、厳密には2.5%~1.5%の間にしか起こらない値だということがわかりました。
データに差がないなら97.5%の確率で発生しない、滅多に起こらないイレギュラーな値です。
有意水準を5%をもって、「A店とB店のラーメンとチャーハンの売れ方に差はない」という帰無仮説を棄却します。
よって、「A店とB店のラーメンとチャーハンの売れ方に差はある」となりました。
![分散分析とF分布表[NOINDEX]](https://www.yuulinux.tokyo/contents/wp-content/uploads/2018/01/bunsan_20181105_1-150x150.jpg)
![平均差の信頼区間とt検定[NOINDEX]](https://www.yuulinux.tokyo/contents/wp-content/uploads/2017/11/sinrai_20181104_1-150x150.jpg)







