もくじ
比率の標本誤差
推計統計学で、とある標本のデータから母集団の値を推計します。
視聴率というものがありますが、日本の全世帯を調査するのは大変ですよね。わずかなサンプル数、今回だと600世帯のサンプルの視聴率から標本誤差を利用すると、全世帯の視聴率(母集団)を確立的に推計することが出来ます。
90%信頼度の比率の標本誤差
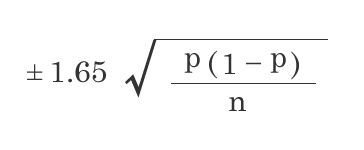
95%信頼度の比率の標本誤差
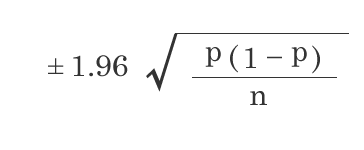
99%信頼度の比率の標本誤差
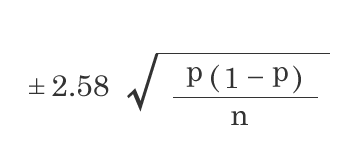
1.65, 1.96, 2.58は標準偏差の個数を表しています。
視聴率を求めよう
600世帯に対して、ある番組の視聴率の統計を取ったところ30%(0.3)でした。母集団との標本誤差95%を求める。
公式にあてはめるだけです。

この場合の全世帯(母集団)の視聴率が95%の確率で26% ~ 34%の範囲に含まれるということがわかります。
サンプル数は600で良いの?
サンプル数を多くすれば誤差の範囲は狭まりますが、60000世帯にしても600世帯との標本誤差の制度は10分の1程度です。
今回の結果を60000世帯とすると、

全世帯(母集団)の視聴率が95%の確率で29.6% ~ 30.4%の範囲に含まれるということがわかります。サンプルを増やすと確かに精度が高くなっていますね!
ただし、労力と誤差とのパフォーマンスから600サンプルがよく利用されています。
![平均差の信頼区間とt検定[NOINDEX]](https://www.yuulinux.tokyo/contents/wp-content/uploads/2017/11/sinrai_20181104_1-150x150.jpg)