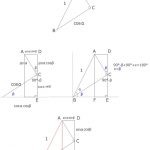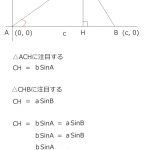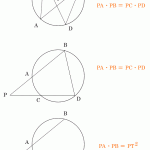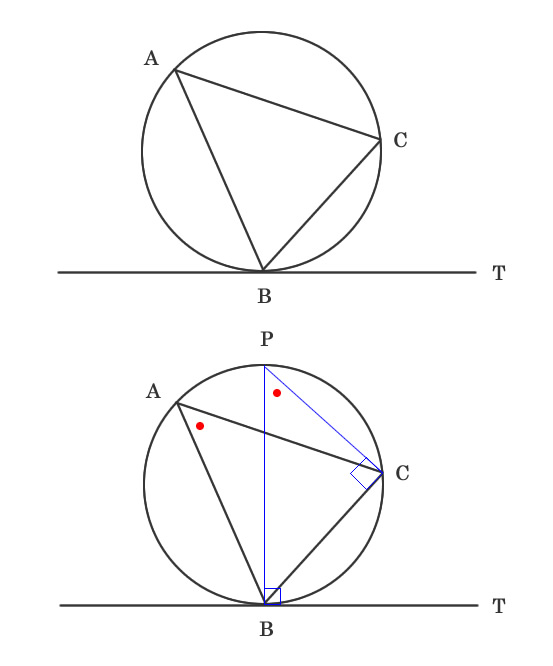
接線Tに対して垂直である円の直径Pの補助線を引くと、
2つの図のようになる。
円周角の定理から
∠CPB = ∠CAB ・・・①
∠CPB + ∠PBC = 90°
∠PBC = 90° - ∠CPB ・・・②
∠CBT = 90° - ∠PBC ・・・③
②と③より、
∠CBT = 90° -(90° - ∠CPB)
∠CBT = 90° -90° + ∠CPB
∠CBT = ∠CPB
①を組み合わせる
∠CAB = ∠CPB = ∠CBT
よって接弦定理を証明できる
∠CAB = ∠CBT