周期Tの関数について、三角関数の和で表現します。
もくじ
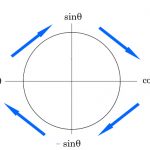
周期2πの時
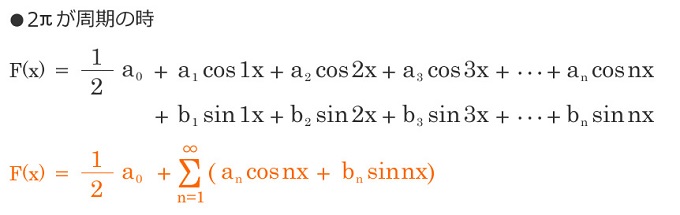
b0はsin0=0になるので省略されるよ!
フーリエ係数
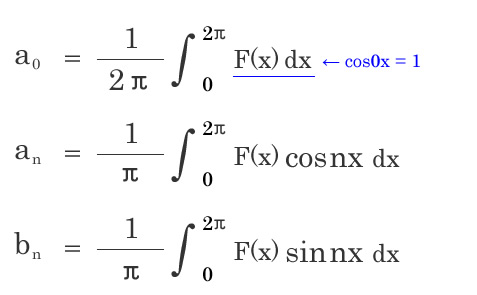
a0, an, bnはフーリエ係数と呼びます。
1/2π? 1/π?
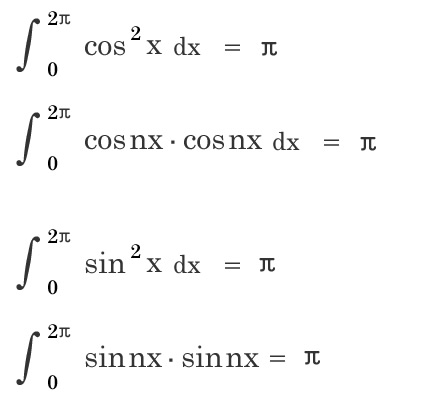

同周期のsin または 同周期のcos同士の関数は直交しないので、周期の区間でも面積πが出ます。
※∫sinx・cosx dx、∫sin2x・sinx dxなど直交している関数の積分において、2πの区間の積分は±の面積の和で=0になります、直交している関数の内積は0になるからです。
anの積分(面積)について、πで割ると一辺である振幅=anが出ます。
a0の時に1/2なのは、n=0の時にcos0で0~2πで積分計算すると2a0になるので、辻褄を合せる為に1/2をかけます。
a0はグラフの全体の上下を決める、
周期2πではない時
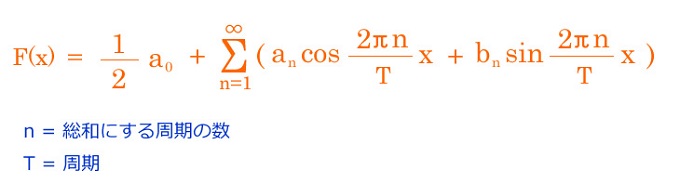
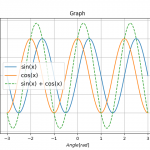
※グラフ等追加します。



![Resolved [mysqlbinlog] ERROR: Got error reading packet from server: Could not find first log file name in binary log index file](https://www.yuulinux.tokyo/contents/wp-content/uploads/2020/04/mysql_logo-150x150.jpg)