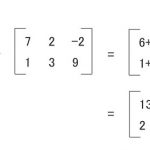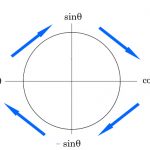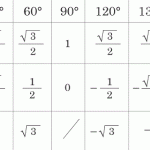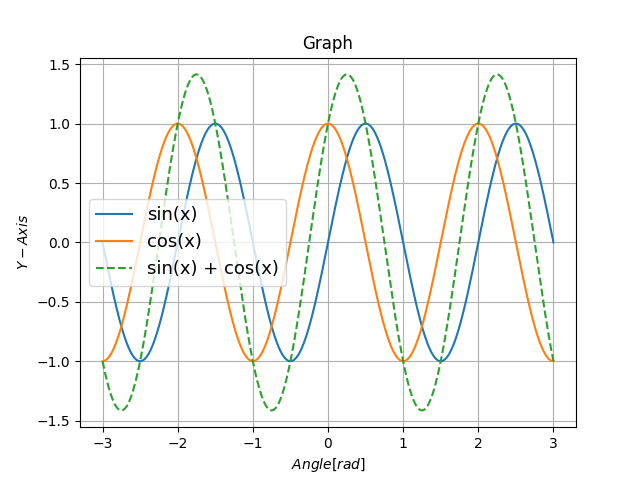
正弦関数と余弦関数の合成のグラフも簡単に作れます。

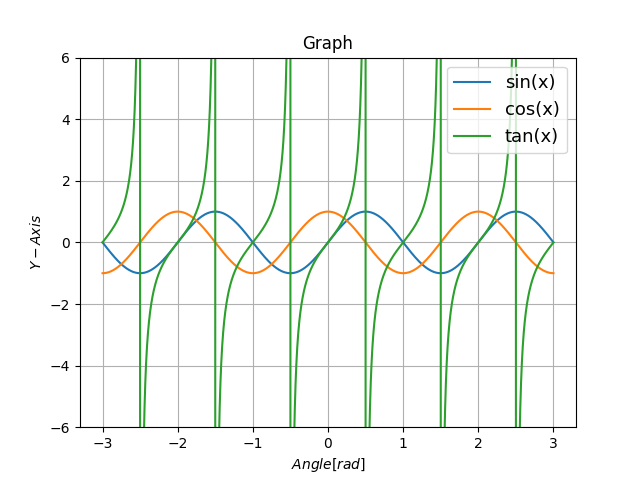
荒ぶる正接関数のグラフ

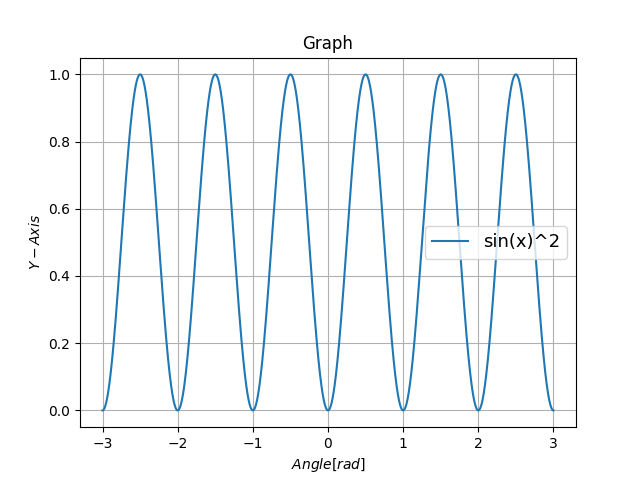
sin(x)同士でかけ合わせることで、－同士の掛け算だから－がなくなります。
周期も1/2になっているね。

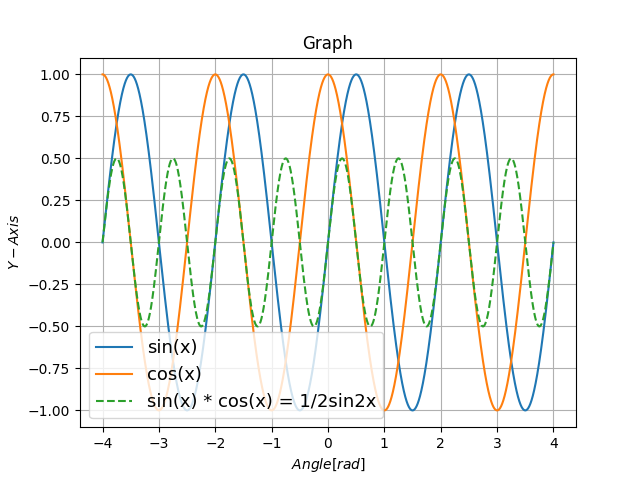
sinxとcosxの積は1/2sin2xになりました、
sinxと比べて、振幅が1/2で、周期は2倍早くなっています。

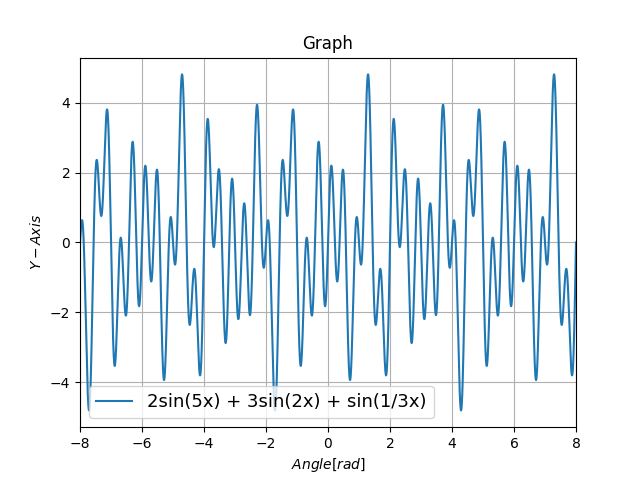
一見複雑ですが、広く見ると周期しています。

# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
import math
import scipy.integrate as spi
import sympy as sym

def main():

    fs = 200000 # サンプル数
    pi = math.pi
    #x  = np.linspace(-20*pi, 20*pi, fs)
    x  = np.linspace(-4*pi, 4*pi, fs)

    sin        = np.sin(x)
    cos        = np.cos(x)
    tan        = np.tan(x)
    sinAddCos  = sin + cos
    sinFoo     = 2*np.sin(5*x) + 3*np.sin(2*x) * np.sin(1/3*x)
    sinProd    = np.sin(x) * np.sin(x)
    sinProdCos = np.sin(x) * np.cos(x)


    plt.plot(x/pi,  sin, label="sin(x)")
    plt.plot(x/pi,  cos, label="cos(x)")
    #plt.plot(x/pi, tan, label="tan(x)")
    #plt.plot(x/pi,  sinAddCos, linestyle="--", label="sin(x) + cos(x)")
    #plt.plot(x/pi, sinFoo, label="2sin(5x) + 3sin(2x) + sin(1/3x)")
    #plt.plot(x/pi, sinProd, label="sin(x)^2")
    plt.plot(x/pi, sinProdCos, linestyle="--", label="sin(x) * cos(x) = 1/2sin2x")

    plt.title('Graph')
    plt.tick_params(labelsize=10)
    plt.xlabel("$Angle [rad]$", fontsize=10)
    plt.ylabel("$Y-Axis$", fontsize=10)
    #plt.xlim([-20, 20])
    #plt.ylim([-6, 6])
    plt.grid()
    plt.legend(fontsize=13) # ラベルの描画
    plt.show()

    plt.savefig('numpy_20180616_32.png')


if __name__ == '__main__':
    main()