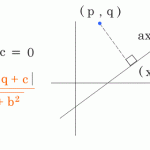もくじ
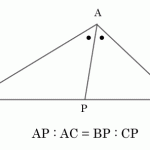
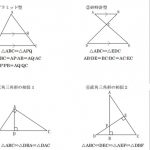
A = Bの証明
- Aの計算結果、Bの計算結果が等しくなった
- A － B = 0になった
- A = C, B = Cになった
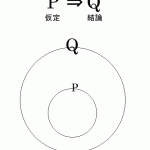
背理法
背理法でA = Bを証明する場合
- A ≠ Bを仮定する
本当に証明したいものの否定系を仮定します。 - A ≠ Bの仮定に矛盾を見つける
- A ≠ Bが矛盾して成り立たなくなる
- 背理法によりA = Bが証明された！
A > Bの証明
A － B を計算して>0であることを示す
- A － B > 0となった
だから、AはBより大きいと証明された
// AがBより大きくないとXはX>0にならないから
不等号の証明
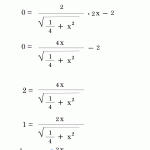
例) x^2 -2x + y^2 + 4y + 5 ≧ 0
- 左辺が0以上
- 左辺 = 0
2点を証明する必要があります。
>例) x^2 -2x + y^2 + 4y + 5 ≧ 0
パターンとして、平方完成して二乗の形にする
(x － 1)^2 －1 + (y + 2)^2 －4 + 5 ≧0
= (x – 1)^2 + (y + 2)^2 ≧ 0
- x = 1, y = －2の時に等号が成立する
- 1の条件を除けば、^2となっているカッコの中は0以上が確定する
よって、
x^2 -2x + y^2 + 4y + 5 ≧ 0
は成立する。
Amazonおすすめ
iPad 9世代 2021年最新作
iPad 9世代出たから買い替え。安いぞ！🐱 初めてならiPad。Kindleを外で見るならiPad mini。ほとんどの人には通常のiPadをおすすめします＞＜