もくじ
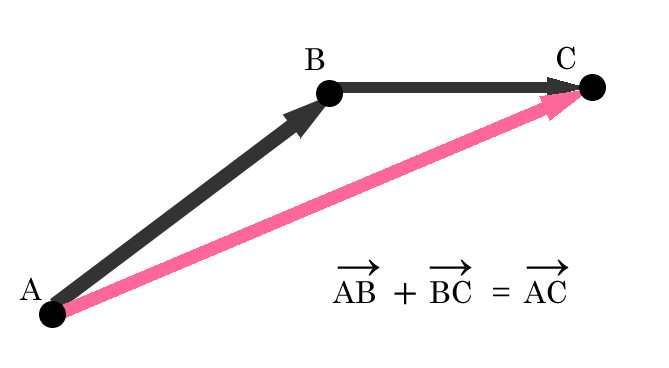
ベクトルの和
出発点と終着点を結ぶ
ABベクトルとBCベクトルの和 = A点とC点を結んだベクトルAC
ベクトルをそれぞれ平行移動すると平行四辺形になる
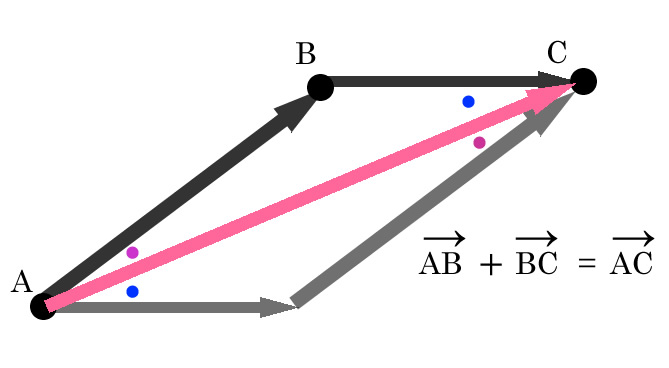
2つのベクトルを平行四辺形を移動して作った対角線がベクトルの和と等しくなる、
また平行な線なのでそれぞれの錯角が等しくなります
ベクトルの差
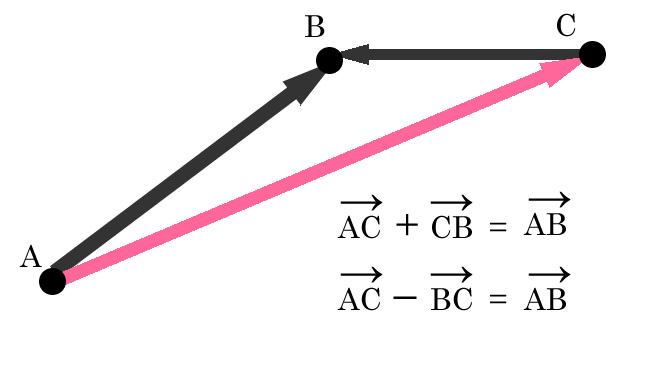
ベクトルの差はベクトルの和で考えることが出来ます、
上記の2つは同じ意味を表しています。
後引く先
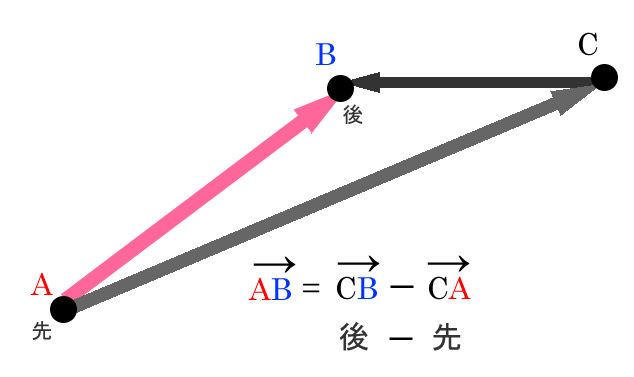
ABベクトルの後と先に点Cからベクトルが結びつくとこうなる。
ABベクトルと点CからA点とB点をベクトルで結んだ時、
「後引く先」で作業的に分解出来る
ベクトルの基本

ベクトルの内積

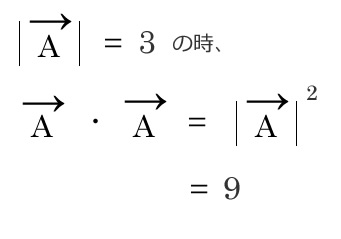
同じベクトル同士の内積の計算
内積が0になる時に直交
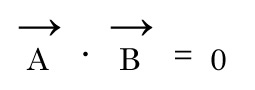
- cosθが0の値になっている
= 2つのベクトルの関係が垂直になっている - 成分を利用して内積を計算した結果が0の場合
2つのベクトルの内積が0の時に直交であることがわかる
レコメンドのアルゴリズム
ベクトルの重心
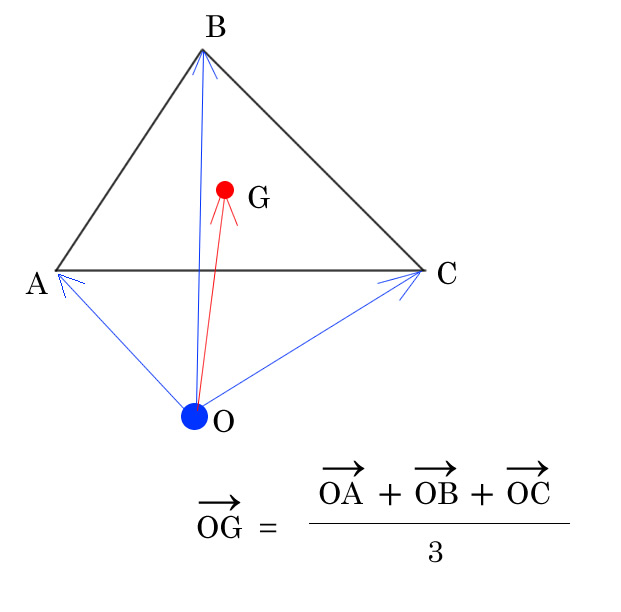
位置ベクトルを利用して導出出来ます、導出は後で書く。
ベクトルの内分
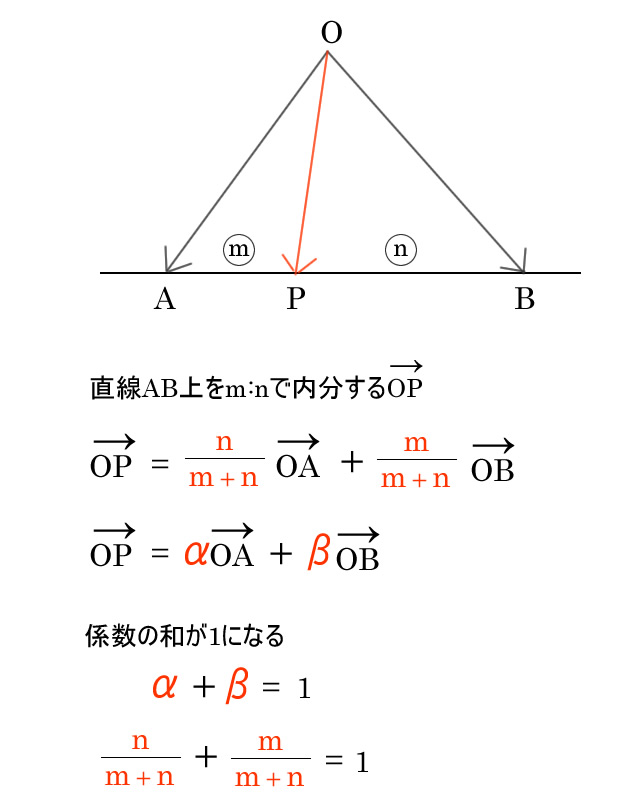
係数の和が1になるのがポイントです。
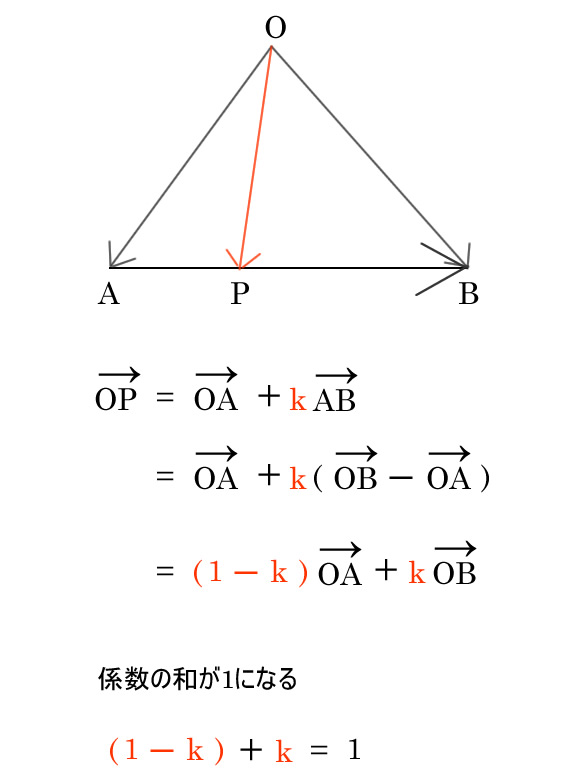
Oを出発点としてベクトルを揃えると整理されます。
ベクトルの外分
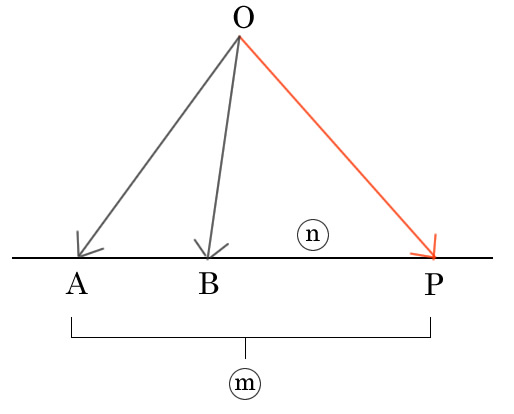

角の二等分線
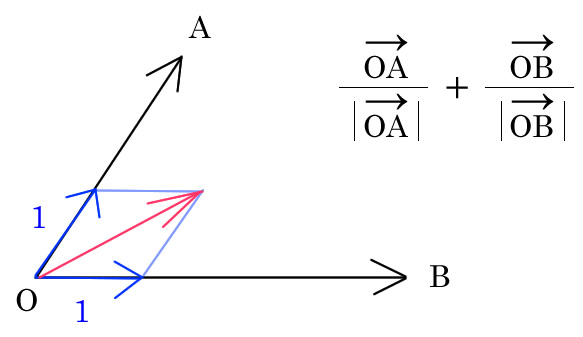
ベクトルの長さがの単位ベクトルにしてそれぞれを和にすることで、ひし形の対角線がベクトルの和になる。
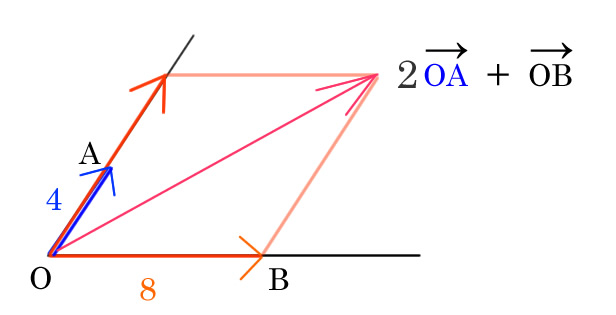
ベクトルの長さを1にすることで揃えてるけれど、要するにひし形にするにはそれぞれのベクトルを同じ長さにすれば同じこと。
この場合はOAベクトルを2倍にして大きさを揃えてあげることで、ひし形が作れます。
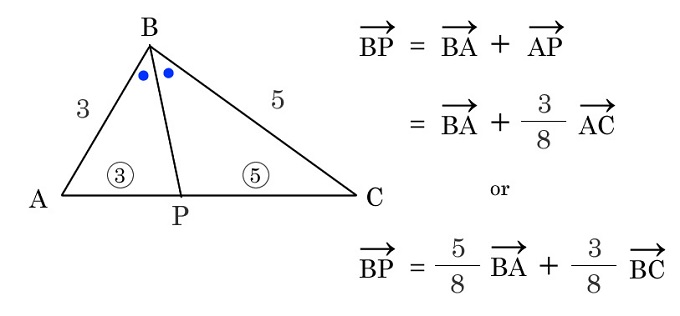
∠ABCの二等分線とACベクトルに交わったP点について考える
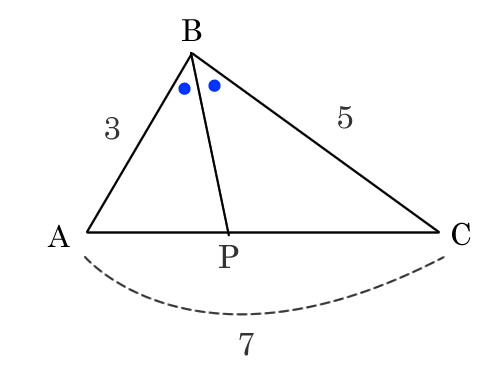
角の二等分線から交わった点で分けられた底辺の比は両辺の比と同一
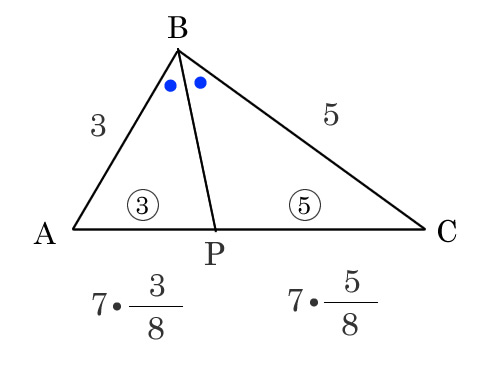
AP : CP = 3 : 5になる、
この定理はベクトルの性質ではないけれど知っていると便利
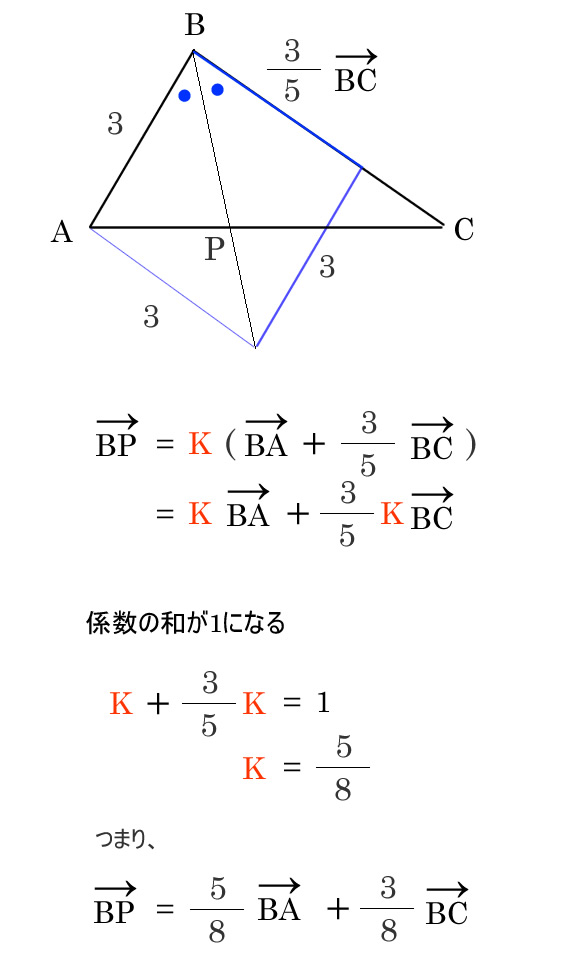
ひし形に補助線を引いて考える
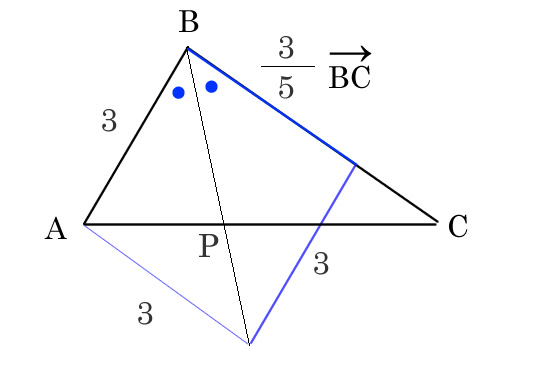
ABベクトルの補助線でひし形を作ってBPベクトルを表現出来る
tの範囲による内分点、外分点の位置
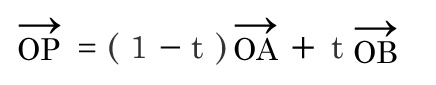
tの値の範囲によって、P点の範囲が決まります。
0 < t <1の時
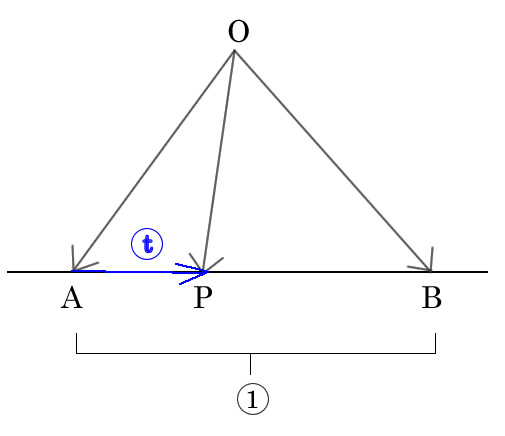
P点は線分AB上にあります。
係数の和が1になる、
(1 - t) + t = 1
t > 1の時
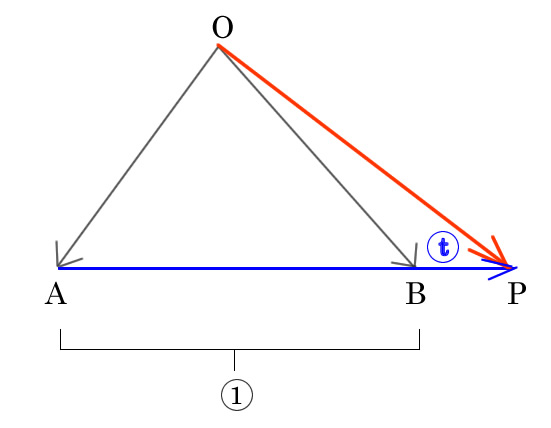
点PはB点を超えて外分点になります。
t < 0の時
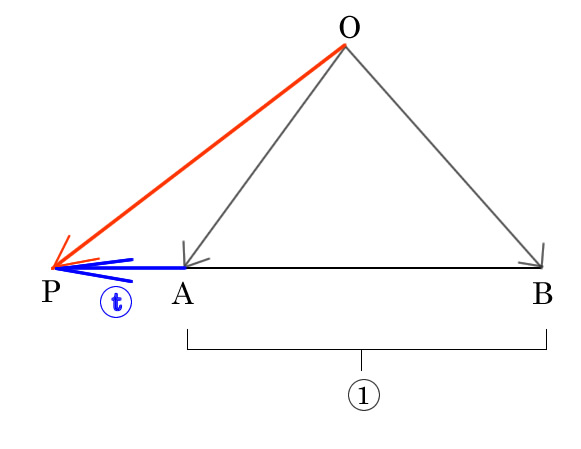
点Pは線分ABの-方向に超えて外分点になります。