• 全体の平均からのずれ = 群間のずれ + 群内のずれ
• 群間の自由度 = 群の数 － 1
• 群内の自由度 = (群1のサンプルサイズ － 1) + (群2のサンプルサイズ － 1) + (群3のサンプルサイズ － 1)
• 全体の自由度 = 各群のデータを合わせたサンプルサイズ － 1
• F値 = 群間の平均平方 / 群内の平均平方

 

信頼区間、有意水準の考え方

• 有意水準0.05 = 信頼区間95%
• 有意水準0.01 = 信頼区間99%
• 有意水準 = 差のない確率
• p値 = 帰無仮説が成立する確率
• p値 < 有意水準α
  差はある ・・・ 帰無仮説を棄却する、差はあるとして対立仮説を採用する → 「有意差がある」という

 

 

F分布表によるF検定

@see http://argent.shinshu-u.ac.jp/lecture/files/pdf/f-table.pdf

 

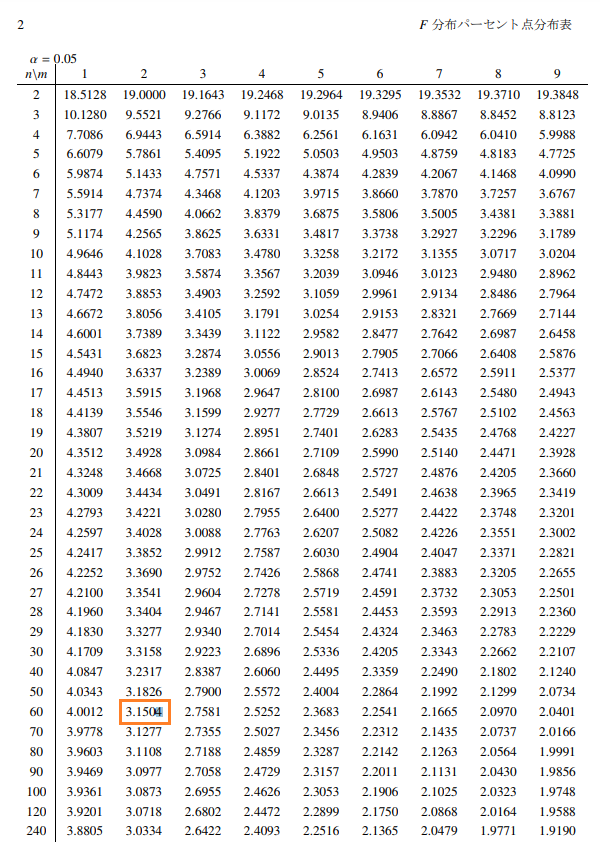
• 有意水準5%のF分布表を参照
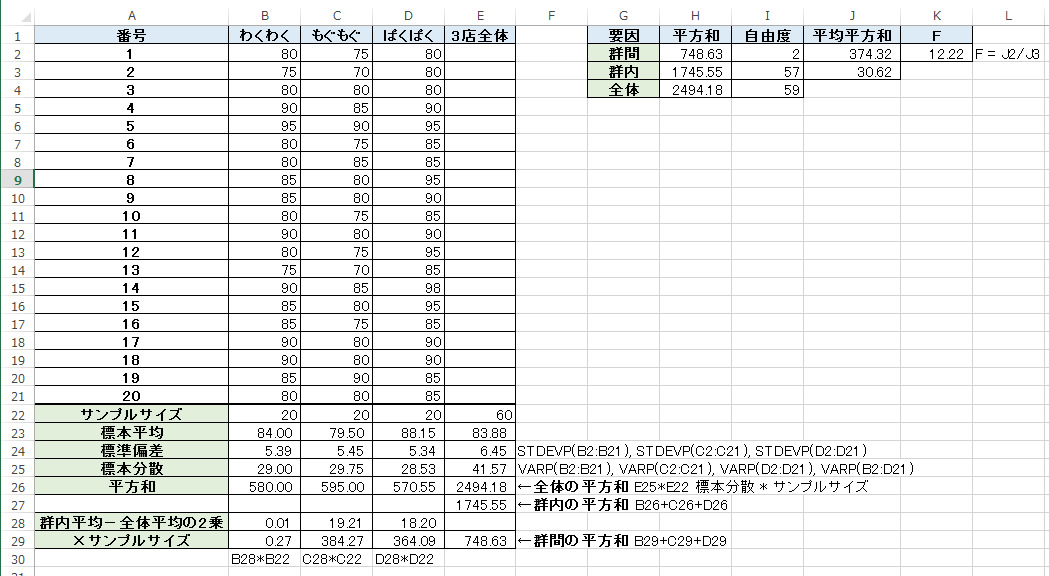
  群間の自由度2, 群内の自由度57かつ群内自由度60の位置 = 3.15
• データのF値 = 12.22

3.15 < 12.22

5%有意水準で“3店のポテトの評価の平均について差はない”が棄却される = 少なくとも1つはデータに差がある

 

// F分布表内にF値が入っていた場合は、
// 帰無仮説 = “群間に差はない”が採用される

 

 

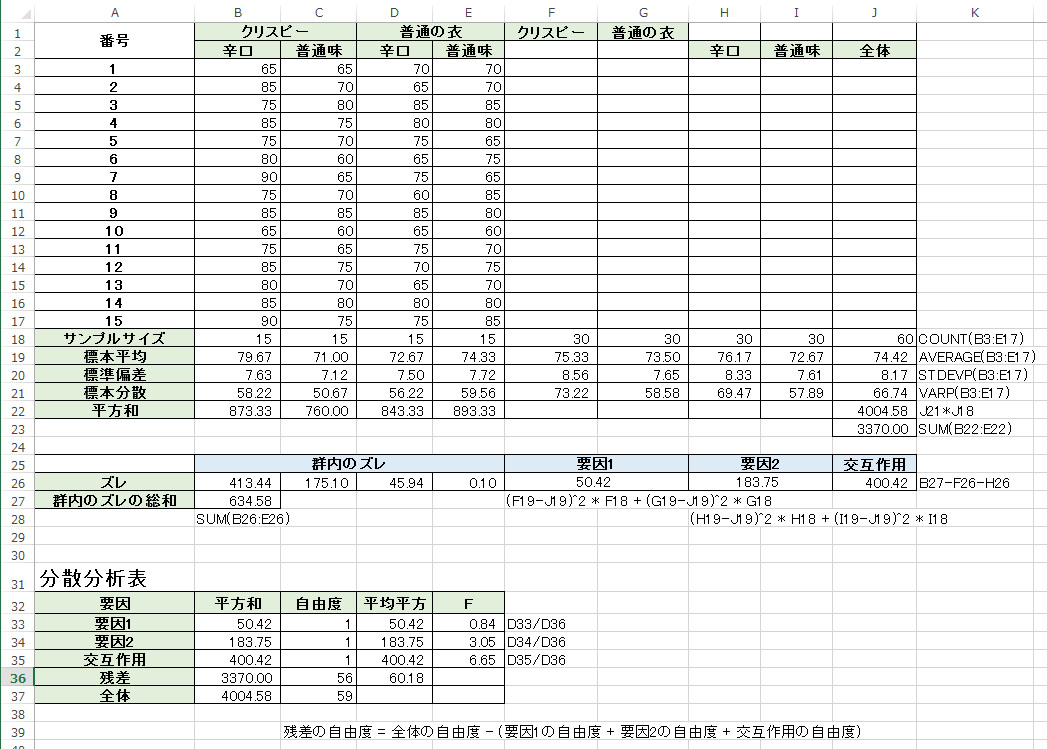
2要因の分散分析

 

 

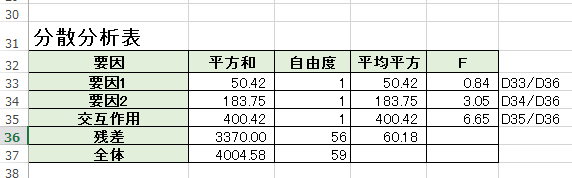
分散分析のF値とF分布表を照らし合わせて棄却域を見ます。

群間の自由度1, 群内の自由度56 ≒ 60にF=0.84
5%の有意水準の時に、F分布表でF= 4.0847となる
= 帰無仮説の棄却域に入らない = 影響しない

要因2もF = 3.05なので
= 帰無仮説の棄却域に入らない = 影響しない

 

交互作用を見るとF=6.65となっており、
= 帰無仮説の棄却域に入る = 棄却できない = 影響がある

「5%有意水準で、交互作用の点数差がある」となります。

 

交互作用

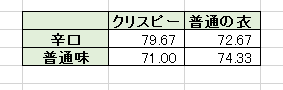
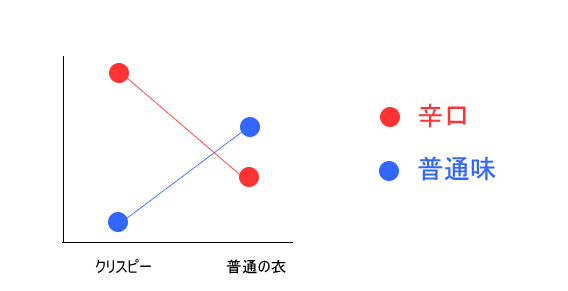
• 衣の種類と味付けは交互差用がある
• 辛口かつクリスピーの評価が高い

 

分散分析により、

味付けと衣の組み合わせは交互さようがあり、
辛口とクリスピーは評価が高いことがわかりました。
よって、
「辛口クリスピー」を売り出していこう！となりました。

 

 

 

@see 統計がわかる