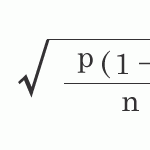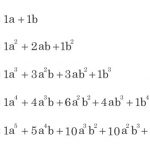t検定

• ２つのグループの平均に差はあるのかそうじゃないか調べる手法
  平均に差がない場合
  95%、または99%の確率で起こりえる差なのでその平均の差に意味はない
  平均に差がある場合
  グループの平均の差は評価の差に意味はある
• グループが3つ以上あるとt検定は使えない

 

 

このページで利用する公式

 

 

差の標準誤差

推定母分散が標本Aと標本Bで等しいものだとすると、

共通因数でくくると、

 

// t分布で利用する

自由度 = (列数2 － 1 ) × {(標本A行数8 － 1) + (標本B行数8 － 1)}

 

 

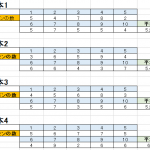
２店の味の評価

対応がない評価によって行った。
対応がない = 16人に1店をインタビュー = サンプル数が異なる場合がある
対応がある = 8人に2店をそれぞれインタビュー = サンプル数が必ず等しくなる

 

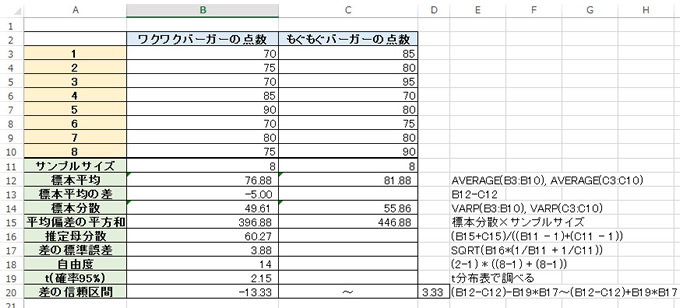
• ２つの店舗の点数があり点数評価を行った
• この２つの標本平均の差は5だった

この標本平均の差5点に意味はあるのか。

 

店舗Aの標本A、店舗Bの標本Bを何度も抽出した時に、
標本A － 標本Bの差も正規分布で表せる = tの信頼区間が出せる

 

t(確率95%)を用いて、平均差の信頼区間の公式に当てはめると、
－13.33 ～3.33
であることがわかった。

• 差が－13 = もぐもぐの評価がかなり高い
• 差が0 = もぐもぐとわくわくの評価に差はない
• 差が+3 = わくわくの方が評価が少し高い

信頼区間に0が含まれていた

95%の確率で評価に差はないことが十分に起こりえる

↓

２店の評価に差はない

 

 

t検定を行います

 

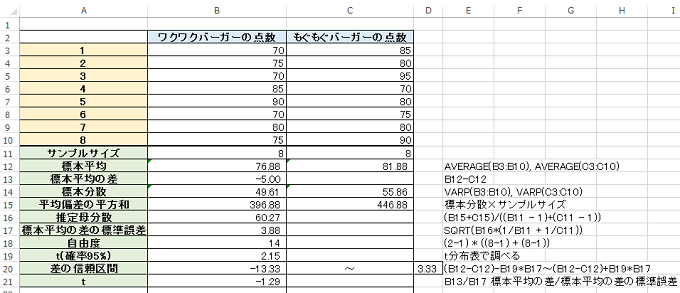
自由度 = (列数2 － 1 ) × {(標本A行数8 － 1) + (標本B行数8 － 1)}

= 14

 

t = 標本平均の差 / 標本平均の差の標準誤差

t = －1.29

 

t分布表

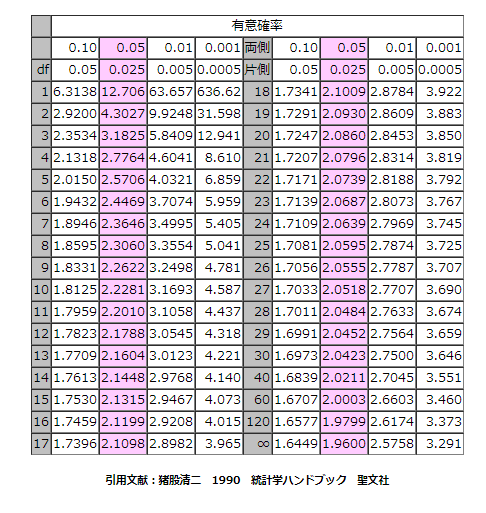
有意確率95%かつ自由度14は2.1448、
今回のデータから求められたtは-1.29

 

95%の確率でtは－2.1448 ～ 2.1448の値の範囲で取る、

標本差の－1.29はこの範囲に値が入っている = 標本の平均に有意な差はない = わくわくばーがーともぐもぐバーガーの点数に差はない

となります。

 

対応のあるt検定

女子高生一人ずつに２店のハンバーガーを評価して貰った場合 = サンプル数が必ず等しくなる

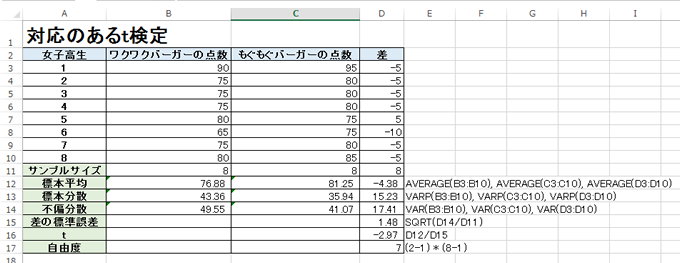
t = 標本平均の差 / 標本平均の差の標準誤差

t = －2.97と出ました。

t分布表

有意確率95%かつ自由度7は2.3646、
今回のデータから求められたtは－2.97

95%の確率でtは－2.3646 ～ 2.3646の値の範囲で取る、

標本差の－2.97はこの範囲に値が入っていない = 標本の平均に有意な差はある = わくわくばーがーともぐもぐバーガーの点数に差はある

となります。

 

平均点の差は無視できない差であり、点数の高いもぐもぐバーガーの方が美味しいとなります。

 

 

なぜ対応のあるなしで結果に差がでたのか？

• 対応のないt検定では、個人間でデータをとるのでばらつきとなる標準誤差が大きくなる
• 対応のあるt検定では、同一個人で評価する為にばらつきとなる標準誤差が小さくなる

対応のあるt検定で調査を行うと有意な差を見出しやすい

 

@see 統計学がよくわかる