実数

実数 ＝ {有理数, 無理数}
有理数と無理数をまとめて実数と呼びます

 

 

有理数

 

整数か分数で表せる

ex)

• 1, 2, 3, ･･･ 100
• 1 = 1/1
• 2 = 2/1
• 3 = 3/1

 

有限小数

ex)

• 0.5 = 1/2
• 0.3 = 3/10
• 1.5 = 3/2

 

 

循環小数

• 0.33333333333・・・ = 10/3

分数で表すことが出来ます。

 

本当に循環小数は分数で表せるの？

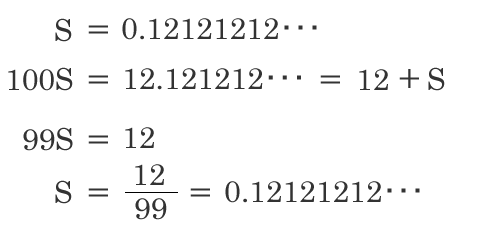
表せます。

 

 

無理数

• 整数でも分数でも表せない
• 循環しない無限小数が無理数

ex)

• √2 = 1.41421356237・・・
• √3 = 1.73205080757 ・・・

 

超越数

• π = 3.14159265359 ・・・
• e = 2.71828182846 ・・・

 

実数ではないもの

• i(虚数)
• 四元数

 

 

 

 

√2が無理数である証明

背理法で証明します。
√2が有理数であることを仮定して、仮定した結果を矛盾させることで無理数であると証明出来ます。

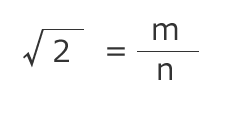
√2が有理数であるならば分数で表現することが出来るので、最大公約数が1となる自然数m, nを使って上記で表してみます。

 

式の両辺をnでかける

√2 × n = m

 

更に２乗します
2n^2 = m^2･･･①

 

2n^2は2でかけているので必ず偶数になります、
そうなるとm^2も偶数であることになります。
つまり、mは偶数です。

奇数は2乗しても奇数でもあるからです。

 

mが偶数であるなら、
m = 2kと表現出来ます。(kは自然数)

 

2n^2 = m^2･･･①に代入すると、

2n^2 = 4k^2

n^2 = 2k^2となります。

 

すると、nもまた偶数ということになります。

これは下記に矛盾します。

√2が有理数であるならば分数で表現することが出来るので、最大公約数が1となる自然数m, nを使って上記で表してみます。

mとnが偶数であるならば、さらに約分することが出来るからです。

 

したがって、√2が有理数であるということは間違いになります。
有理数でないならば、無理数であるということになります。

 

 

 

@see

• Newton 虚数がよくわかる