疑似乱数

平方採中法

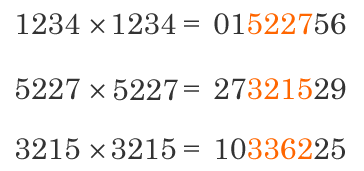
･･･使わない(۶•̀ᴗ•́)۶

線形合同法

乱数列の生成は次の漸化式を用います。

X_n+1 = (A * X_n + C) mod M

A, C, M は定数とし、それぞれ M>A, M>B, A>0, B≥0 でなければなりません。 X₀ はSeed値として与えられることとします(とりあえず 0 や 1 でも構いません)。乱数の出現範囲は最大で 0～M となります。

一例

具体的に適当な値を当てはめて乱数列を生成してみましょう。ここでは A=3, C=4, M=11, X₀=1 とします。では漸化式に当てはめていくつかの乱数を生成します。

X₁ = (3 * 1 + 4) mod 11 = 7

X₂ = (3 * 7 + 4) mod 11 = 3

X₃ = (3 * 3 + 4) mod 11 = 2

X₄ = (3 * 2 + 4) mod 11 = 10

X₅ = (3 * 10 + 4) mod 11 = 1

X₆ = (3 * 1 + 4) mod 11 = 7
@see http://algoful.com/Archive/Algorithm/LCG

1950年頃、Derrick Henry Lehmerという人がこのアルゴリズムを作りました。
ただ、これはゲーム業界において非常に悪名高いアルゴリズムでもあります。
皆さんは「カルドセプトサーガ」というゲームをご存じでしょうか。
これはサイコロを振って進むモノポリー型のカードゲームですが、サイコロの規則性があったことで一躍有名になりました。
特定の条件を満たした場合、サイコロは奇数と偶数を交互に出してしまったり、
次の出目が予測可能な状況になったりする現象があったためです。
これは線形合同法で実装された乱数の最下位ビットが0と1の繰り返しになることに起因したり、
同じ順序の数列が必ず生成されるということに起因しています。
@see https://qiita.com/isonami/items/1cc278cbf2093d2d6abd

･･･使わない(۶•̀ᴗ•́)۶

メルセンヌ・ツイスター

標準。

Pythonだとrandom()
PHPだとmt_rand()

周期：2^19937 − 1 ≒ 4.3 × 106001
• 1周期で623次元空間に均等分布することが証明
（32ビット精度で）
• 生成速度は、近年の線形合同法（ mod 248）よりも高速
• 多くの計算機言語で標準擬似乱数として採用(Python, Ruby,
R, PHP, MATLAB, C++（C++11から）など)
他、広く用いられている
（多くのソフト、ポケモンゲーム、任天堂Wiiなど）

メリット：
• 周期を長くしても、生成速度が遅くならない
「二か所見て、足して、一か所に書く」という動作だから
xn+607 = xn+273 + xn
• 周期が極大なので、「全て0」以外のビットパターンが
(xn, . . . , xn+607−1
) (n = 1, 2, . . . , 2
607 − 1)
のなかにちょうど一度だけ現れる（607次元均等分布性）

@see http://www.math.sci.hiroshima-u.ac.jp/~m-mat/TEACH/ichimura-sho-koen.pdf