グループ分けを行い、各グループの類似度をベクトルの内積の公式を使って、cosθの値で類似度を判断する。

 

• 類似度が高い･･･似てるほど1に近づく、類似度100%で1
• 類似度が低い･･･似てないほど0に近づく、類似度0%で0

 

 

補足1. ベクトルの基本的なところ

 

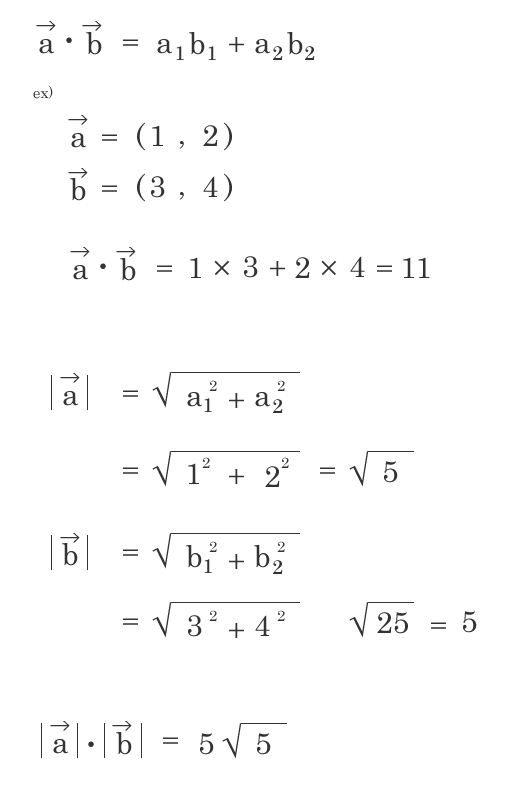
補足2. ベクトルの内積の公式

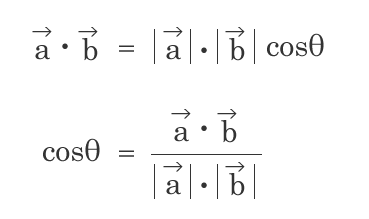
• a, bベクトルのなす角θが直角である時にcos90° = 0であり、
  a, bベクトルがそれぞれどのような長さの値でも、内積は0になる性質があります。
• a, bベクトルのなす角θが0°である時にcos0° = 1であり、
  a, bベクトルの内積は一辺が|a|の大きさ, 一辺が|b|の大きさの長方形の面積と等しくなります。

 

 

 

補足3. ベクトルの正規化, 単位ベクトル

 

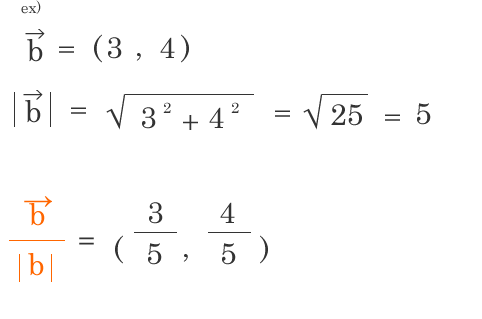
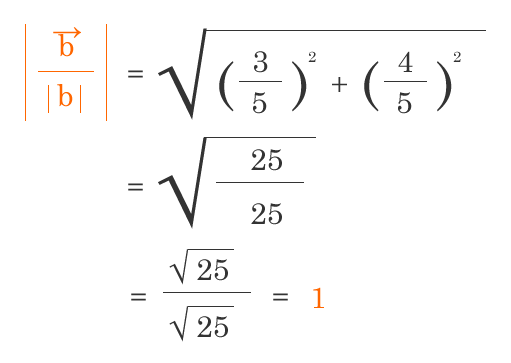
ベクトルの成分に対して、ベクトルの大きさで割ることで大きさ1の成分が出せます。ベクトルの方向を変えずに大きさを1にする操作を正規化と呼びます。

 

• 大きさが1のベクトルを単位ベクトルと呼ぶ
• ベクトルの正規化
  ベクトルをそのベクトルの長さで割ると、単位ベクトルを取得できます
• ベクトルの内積の公式
  単位ベクトルに変換した大きさ1同士のベクトルの内積がcosθということですね。

 

補足4.  cosθって何者？

 

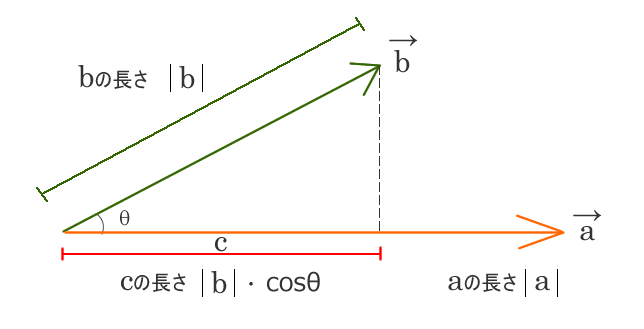
bの長さの屋根から出来る影をcの長さとして見ると、
cosθはbの長さがcの影になった時の縮小率として捉えることが出来ますね。

 

内積は屋根が作る影と地面の大きさとの掛け算

| b | が | a |につくる影の長さ = C = | b | ・ cosθ

ベクトルa ・ ベクトル b = | b | ・ cosθ × | a | 

 

 

 

単位円の時、cosθは影の長さ

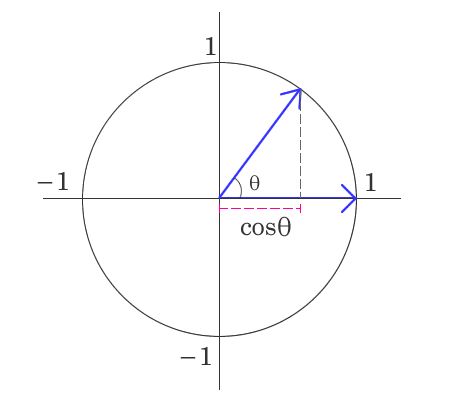
成分が負(－)を含まない場合 θ = 0～90°, 0 ≦ cosθ ≦ 1

• ベクトル同士が完全に同じ方向の時はθ = 0°, cos0°= 1
• ベクトル同士が全く異なる場合はθ = 90°, cos90° = 0

 

※ 成分が負を含む場合 θ = 0~180°, -1 ≦ cosθ ≦ 1

• ベクトル同士が完全に逆向きの時はθ = 180°, cos180° = -1

 

 

ベクトルの内積はどれだけベクトル同士が同じ方向を向いているか = 類似度、この性質を利用します。

 

 

補足5.  n次元

軸が3つの空間ベクトルが軸が2つの平面ベクトルと同じ要領でベクトル計算出来たように、n次元に関しても同様に計算出来ます。

 

 

 

実際にやってみよう！ 好きなフルーツの例

	ばなな	もも	ぶどう	りんご
Aさん	1	1	1	0
Bさん	1	0	1	0
Cさん	1	1	1	0
Dさん	0	1	0	1
Eさん	1	0	0	1
Fさん	1	0	1	1

 

• 1 = 好き
• 0 = 興味なし

 

ばなな好きグループの合算値

構成データ：A, B, C, E, Fさん

 

	ばなな	もも	ぶどう	りんご
ばなな好き	5	2	4	2

 

 

各グループの合算値

	ばなな	もも	ぶどう	りんご
ばなな好き	5	2	4	2
もも好き	2	3	2	1
ぶどう好き	4	2	4	1
りんご好き	2	1	1	3

 

 

プログラムで計算しよう

 

# coding: utf-8
import numpy as np

# ベクトル正規化
def normarize(v):
    return v / np.linalg.norm(v)

# cos類似度
def cos_similarity(v1, v2):
    return np.dot(v1, v2)


if __name__ == '__main__':

    bananaZuki = np.array([ 5, 2, 4, 2 ])
    momoZuki   = np.array([ 2, 3, 2, 1 ])
    budouZuki  = np.array([ 4, 2, 4, 1 ])
    ringoZuki  = np.array([ 2, 1, 1, 3 ])

    n_bananaZuki = normarize(bananaZuki)
    n_momoZuki   = normarize(momoZuki)
    n_budouZuki  = normarize(budouZuki)
    n_ringoZuki  = normarize(ringoZuki)


    print( 'ばなな好き・もも好き:',   cos_similarity(n_bananaZuki, n_momoZuki) )
    print( 'ばなな好き・ぶどう好き:', cos_similarity(n_bananaZuki, n_budouZuki) )
    print( 'ばなな好き・りんご好き:', cos_similarity(n_bananaZuki, n_ringoZuki) )

    print( 'もも好き・ぶどう好き:',   cos_similarity(n_momoZuki, n_budouZuki) )
    print( 'もも好き・りんご好き:',   cos_similarity(n_momoZuki, n_ringoZuki) )

    print( 'ぶどう好き・りんご好き:', cos_similarity(n_budouZuki, n_ringoZuki) )

 

Numpy

• ベクトルの内積: nunpy.dot(v1, v2)
• ベクトルの長さ: numpy.linalg.norm(v1)

Functions

• 正規化：normarize(v)
• cos類似度: cos_similarity(v1, v2)

 

 

# python3  cosSimFruit.py

ばなな好き・もも好き: 0.875465538611916
ばなな好き・ぶどう好き: 0.9863939238321437
ばなな好き・りんご好き: 0.8114822249196492
もも好き・ぶどう好き: 0.891231897035948
もも好き・りんご好き: 0.7302967433402215
ぶどう好き・りんご好き: 0.7216098119626152

 

 

類似度

	ばなな好き	もも好き	ぶどう好き	りんご好き
ばなな好き	1	0.875	0.986	0.811
もも好き	–	1	0.891	0.730
ぶどう好き	–	–	1	0.721
りんご好き	–	–	–	1

ばなな好きグループとぶどう好きグループの好みはほとんど同じだということがわかります。