もくじ
中央値(メジアン)
サンプル数が奇数の場合
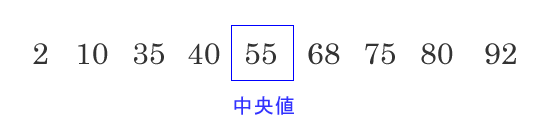
サンプル数が偶数の場合

中央の数値2つの平均を中央値とします。
四分位数(ヒンジ), 四分位範囲(IQR)

- 第1四分位点(Q1)
- 第2四分位点(Q2)
- 第3四分位点(Q3)
四分位範囲(IQR) = 第3四分位数(Q3) - 第1四分位数(Q1)
四分位偏差
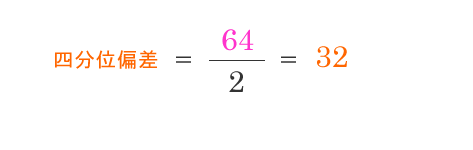
「箱ひげ図」で視覚化しよう
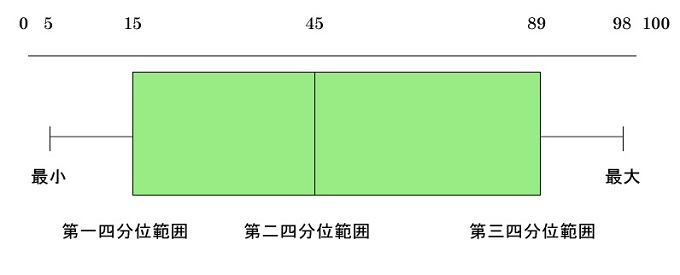
わかりやすいですね。
はずれ値
- 第一四分位数 - (四分位範囲 × 1.5) 以下の数字
Q1 - (IQR × 1.5) - 第3四分位数 + (四分位範囲 × 1.5) 以上の数字
Q3 + (IQR × 1.5)
※はずれ値だからといってどのような場合でも除外して良いということはありません。
なぜそのはずれ値が出たのか考えて、計測ミスならはずして良い。
四分位範囲? 四分位偏差?
どちらもデータのばらつきを表します。
四分位範囲と四分位偏差のメリット
- はずれ値の影響を受けにくい
- 四分位範囲からはずれ値を出せる

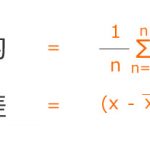


![Plesk12.5.30 25番で待ちうけさせる status=deferred (connect to example.com[111.xxx.yyy.2]:25: Connection refused)](https://www.yuulinux.tokyo/contents/wp-content/uploads/2017/10/plesk25_201710027_2-150x150.jpg)