テイラー展開
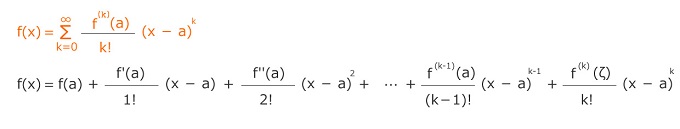
元の式 = f(a) + 1階微分 + 2階微分 + ・・・ + n階微分した総和
数があまりに小さい時に近似として使える。
物理学・統計学、三角関数等を簡単な近似の式にする。
exp)
(1.008)^20
0次近似
1.008^20はほとんど1と同じという考え
1.008^20
≒ 1^20
≒ 1
1次近似
(1.008)^20 = (1 + 0.008)^20
≒ (1 + x)^20とします。
近似にする手段として接線の公式を利用します。
f(x) = f(a) + f'(a)/1!(x-a)
(1 + x)^20 = (1 + a)^20 + 20(1 + a)^19/1! × (x -a)
マクローリン展開
計算を簡単にする為にaが0の時で計算してみる、
原点周りでの展開で簡単にすること=マクローリン展開
a=0とすると、
(1 + 0)^20 + 20(1 + 0)^19 × (x – 0)
= 1 + 20×1^19 × x
= 1 + 20x
xが0.008だから、
= 1 + 20 × 0.008
= 1 + 0.16
=1.16
(1.008)^20の0の周りのテイラー展開での1次近似は1.16
(1.008)^20をまともに計算すると下記
1.17276404348
1.1727… ≒ 1.16
また、高次の導関数を考慮すると、近似はより近くなる。
2次近似
f(x) = f(a) + f'(a)/1!(x-a) + f”(a)/2!(x-a)^2
(1 + x)^20 = (1 + a)^20 + 20(1 + a)^19/1! × (x -a) + 20 × 19(1 + a)^18/2! × (x -a)
マクローリン展開
(1 + x)^20 = + (1 + 0)^20 + 20(1 + 0)^19/1! × (x – 0) + 19(1 + 0)^18/2! × (x -0)^2
= 1 + 20x + 19/2! × x
= 1 + 20x + 9.5x^2
f(0.008) = 1 + 20 × 0.008 + 9.5 × 0.008^2
=1.160608









 初めてならiPad。Kindleを外で見るならiPad mini。ほとんどの人には通常のiPadをおすすめします><
初めてならiPad。Kindleを外で見るならiPad mini。ほとんどの人には通常のiPadをおすすめします><