順列と組み合わせの違い

 

• 5人の中から２人並べる･･･順列 = 順番を気にする組み合わせ、名前をつけて区別できる組み合わせ。
• 5人の中から２人選ぶ･･･組み合わせ = 順番を気にしない組み合わせ

 

 

 

 

順列 順番を気にする組み合わせ nPr

 

要素が同じ場合

 

nPn = n!

4人が4つの椅子に座る順番

 

4! = 4×3×2×1 = 24通り

 

 

要素が異なる場合

nPrは順列を示していて、n個のなかからｒ個選んで並べた総数

nPr = n!/(n-r)!

 

(ex)

5人が3つの椅子に座る組み合わせ ※順番を気にする組み合わせ

 

5×4×3×2×1 / (5-2)! = 120 / 3×2×1 = 20通り

 

 

(ex)

1, 2, 3, 4, 5と書かれた5枚のカードから３つ取り出して、３桁の整数を作り出す組み合わせ

 

5!/(5-3)! = 24 = (5 × 4 × 3 × 2 × 1) / (2 × 1) = 5 × 4 × 3 = 60通り

 

 

(ex)

1, 2, 3, 4, 5, 6, 7の数字を並び替えて3桁の数字はいくつ作れる？

7P3 = 7 × 6 × 5 = 210通り

 

(ex)

1, 2, 3, 4, 5, 6, 7の数字を並び替えて、3桁の偶数はいくつ作れる？

 

偶数にするには、一の位が2, 4, 6になるから、

百の位･･･1, 2, 3, 4, 5, 6, 7
十の位･･･1, 2, 3, 4, 5, 6, 7から百の位で使っていないもの

しかし、一の位で1つ数字を使わないといけないから、
百と十の位の順列はつまり、
6つの数字を使って2桁の並びるのと同じ = 6P2

一の位･･･2, 4, 6の3通通り
つまり、3つの数字を使って1つ並べる組み合わせ絵のと同じ

6P2 × 3P1 = 6!/(6-2)! × 3!/(3-1)! = (6 × 5) × 3 = 90通り

 

 

(ex)

1, 2, 3, 4, 5, 6の数字を使って6桁の奇数はいくつ作れる？

 

1の位は1, 3, 5の順列で3P3 = 3 × 2 × 1 = 6通り

後は1の位で使った数字を覗いて、5桁に5つの数字を並び変える組み合わせだから、
5P5 = 5 × 4 × 3 × 2 × 1 = 120通り

 

5P5 × 3P3 = 120 × 6 = 780通り

 

 

 

(ex) 5人のキャラから勇者、魔法使い、遊び人を決める

 

名前やカテゴリで区別するのも順列です。
5P3 = 5 × 4 = 20通り

 

 

(ex)

男子2人、女子5人において、男子が両端になる並びはいくつ？

 

●○○○○○●

男子の2人の並び変え= 2P2 = 2通り

女子5人の並び変え= 5P5 = 120通り

 

2P2 × 5P5 = 240通り

 

(ex)

男子2人、女子5人において、男子が隣あう並びはいくつ？

●●○○○○○ or ○●●○○○○ or ･･･

男子の2人の並び変え= 2P2 = 2! = 2通り
男子のペアを1人と考えると、6人の並べ変えになる = 6P6 = 6! = 720通り

 

2P2 × 6P6 = 2 × 720 = 1440通り

 

 

(ex)

男子2人、女子5人において、男子が隣合わない並びはいくつ？

 

事象で考える解法

• 余事象 = 全事象 － 事象
• 男子が隣合わない並び = 全体の組み合わせから男子が隣あう組み合わせを引いたもの

 

7P7 － 1440 = 3600通り

 

順列で考える解法

^○^○^○^○^○^

^の場所に●●を入れていく

 

^の数 = 6つ
6つの隙間に2人の男子を入れる組み合わせ = 6P2 = 30

女子を5人並べる組み合わせ = 5P5 = 5! = 120

6P2 × 5P5 = 3600通り

 

 

重複順列 何度同じものを使っても良い場合の順列

 

パターンがnでr回試行した時は何通りか？
n^r

 

(ex)

コインを5回投げて表か裏の組み合わせ

 

2^5 = 2 × 2 × 2 × 2 × 2 = 32通り

表や裏は何度でも出ても良いからこうなります、
他には〇✖、〇✖△となったr回試行の場合も重複順列

 

ex)

1,2,3,4の4つの数字で5桁の整数を作る、同じ数字は何度も使っても良い場合。

 

4^5 = 1024通り

 

 

(ex)

1,2,3,4の4つの数字で5桁の整数を作る、奇数の場合は？
同じ数字は何度も使っても良い場合。

 

奇数は一の位が1と3の2通り。
4^4 × 2 = 512通り

 

ex)

0, 1, 2, 3を使って3桁の整数を作る

百の位･･･ 1, 2, 3 = 3通り
十の位･･･ 0, 1, 2, 3 = 4通り
一の位･･･ 0, 1, 2, 3 = 4通り

3 × 4 × 4 =  48通り

 

 

(ex)

A, B, C, Dさんを選んでグループを作る、グループの人数は1人でも良いが選ばなければいけない。何通りか。

 

Aさんを選ぶ、選ばない = 2通り
Bさんを選ぶ、選ばない = 2通り
Cさんを選ぶ、選ばない = 2通り
Dさんを選ぶ、選ばない = 2通り

2^4

誰も選ばない = １通り

 

2^4 － 1 = 15

 

 

円順列

 

 

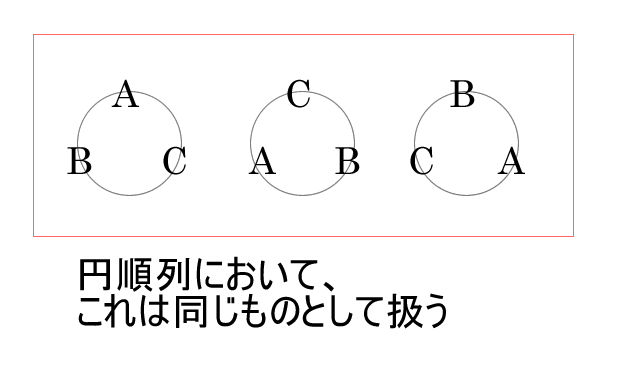
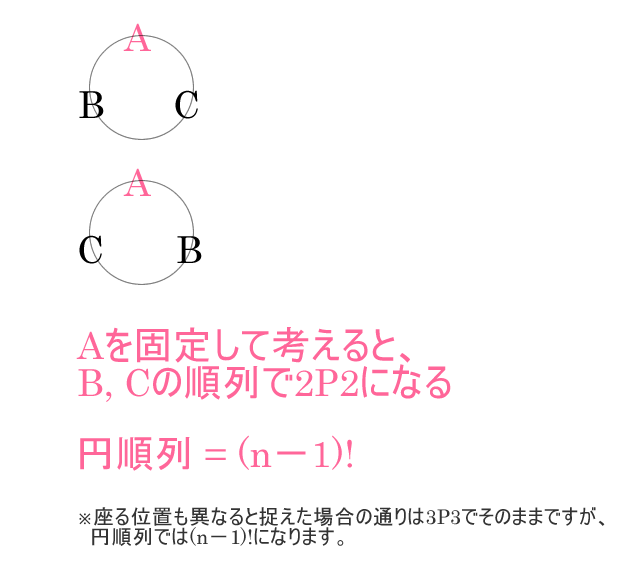
円順列ではどこかを固定してから考えるのが大切。
固定したものを考えてから残りの余ったもので単純な順列を考えるから、
(n － 1)!の順列になるのです。

 

 

(ex1)

カップル2人と他の客5人の7人が円卓に座るのは何通り？

 

(7－1)! = 6! = 720通り

 

(ex2)

カップル2人と他の客5人の7人が円卓に座る、カップルが隣合わないのは何通り？

 

 

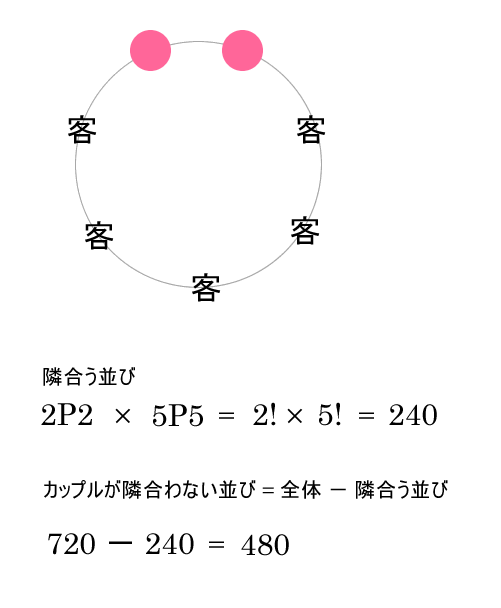
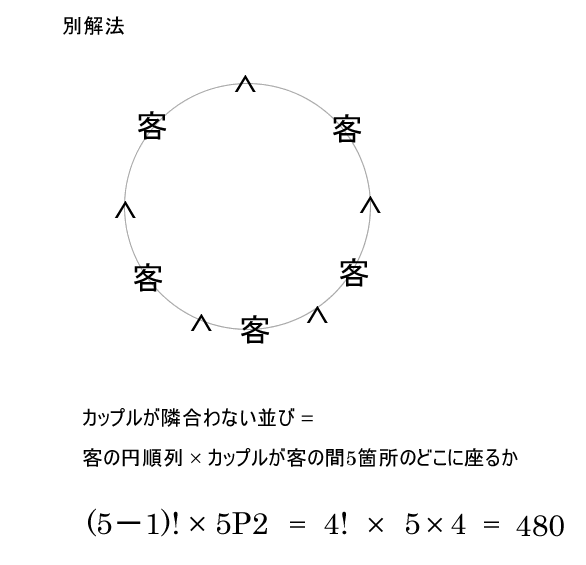
数珠順列

 

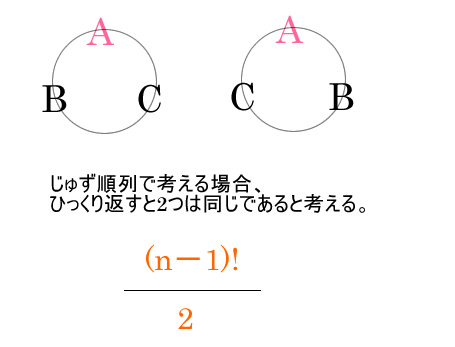
重複した要素のある順列

 

最短経路

 

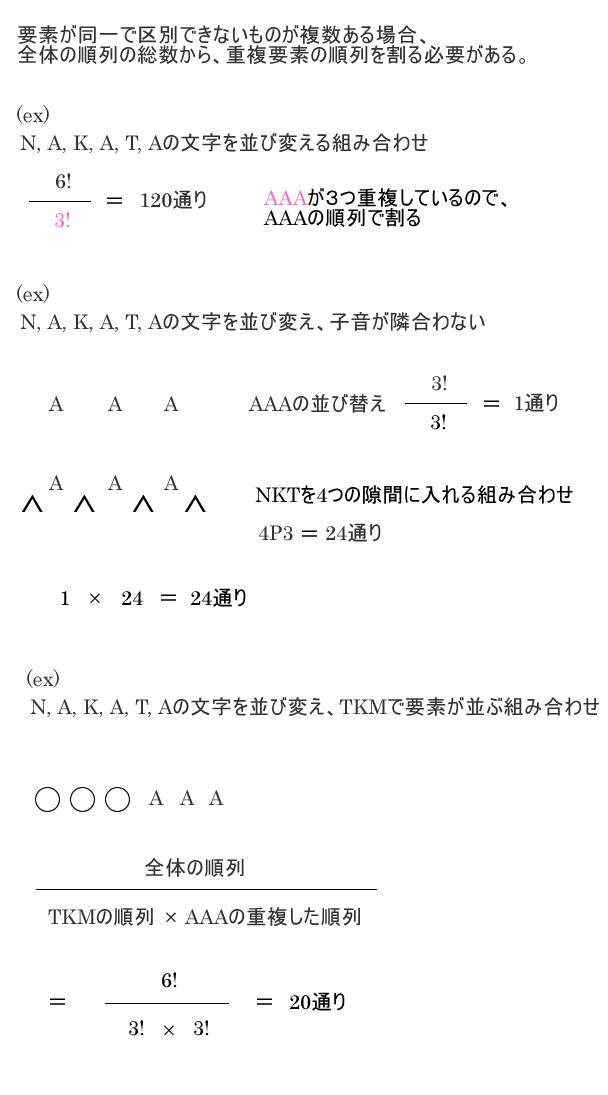
最短経路

 

 

 

 

順番を気にしない組み合わせ nCr

nCrは組み合わせを示していて、n個のなかからr個を１組として取り出したときのパターンの総数

nCr = n!/(n-r)!r!

 

 

5人の中から３人を選ぶ

 

5!/3!(5-3)!  =  120/2! × 3 × 2 × 1 = 120/12 = 10通り

 

 

 

男5人, 女4人の中から3人選ぶ

 

組み合わせの総数

9C3 = 9!/3!(9-3)! = 84通り

 

女子が少なくとも1人含まれる選び方

=すべての組み合わせから、男だけの組み合わせを引く

5C3 = 5!/3!(5-3)! = 10
83 – 10 = 73通り

 

男子1人、女子２人選んで１列に並べる方法

5C1 × 4C2 × 3P3
= 5!/1!(5-1)! × 4!/2!(4-2)! × 3!/(3-3)!
= 5 × 6 × 6 = 180通り

 

 

重複組み合わせ

 

重複組み合わせ